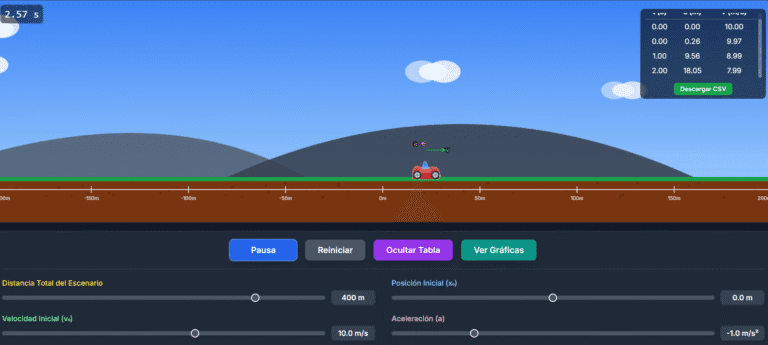
Simulador de caida libre

🧪 Laboratorio de Caída Libre

En este simulador interactivo de caída libre podrás experimentar cómo actúa la gravedad en diferentes planetas, añadir rozamiento con el aire y visualizar en tiempo real cómo cambian la posición y la velocidad de un objeto al caer.
👉 Explora el Simulador de Tiro Vertical

Categoría Física > Cinemática

Nivel educativo ESO

Dificultad Media (4/10)

🔗 Categoría: Física | Cinemática ↗️
🎓 Nivel educativo: ESO
⚙️ Dificultad: Fácil (3/10)
📈 Visitas: 1005

📎 Código para incrustar

¿Eres profe, divulgador o webmaster?
Puedes incrustar esta simulación en tu web o blog sin problema.

Solo pedimos dos cosas básicas:

✅ Que cites la fuente: AulaQuest.com
🚫 Que no la uses con fines comerciales

Este es el código que puedes copiar:

<iframe
  src="https://sim.aulaquest.com/fisica/caida-libre.html"
  width="100%"
  height="560"
  style="border: 1px solid #ccc; border-radius: 8px;"
  allowfullscreen
  title="Simulación de caida libre"></iframe>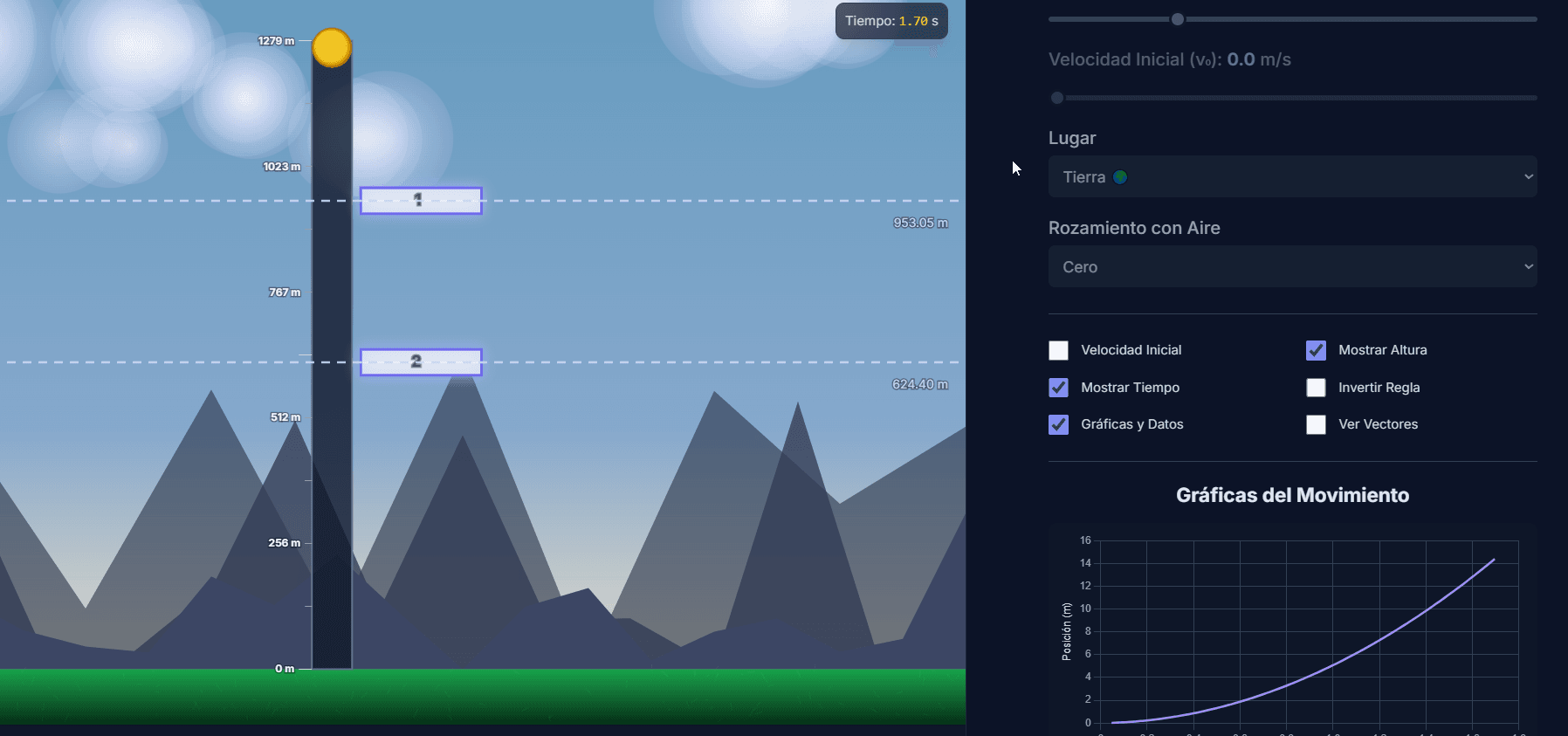

[boton_favoritos]

Vista previa de la Simulación de caida libre

AulaQuest

Iniciando simulación...

Caída Libre: Del Ideal al Real con Aula Quest

Hola a todos y todas, qué bien teneros por aquí, estudiantes de Aula Quest, para otra exploración. Hoy nos metemos de lleno, pero de lleno, con un tema clave en física: la caída libre.

Y lo guay es que esta charla viene con compañía, una simulación interactiva que tenéis ahí mismo, disponible. O sea, que mientras hablamos podéis ir toquiteando, probando cosas, viendo la física pasar delante vuestro.

La misión de hoy es sencilla: pillar bien qué es esto de la caída libre, cómo funciona por dentro y, sobre todo, cómo usar la simulación para analizarla a fondo. Okay, vamos a desglosar esto.

Exacto. Y esa es, ¿eh?, la magia de una buena simulación, ¿no? Que convierte esas ecuaciones que a veces en la pizarra son un poco abstractas, quizá, en algo que puedes ver, tocar, con lo que puedes interactuar.

Es como tener un mini laboratorio en casa.

Me gusta eso del mini laboratorio. Pues, empecemos por el principio, por lo básico. ¿Qué es exactamente la caída libre ideal? Porque eso de "ideal" suena a que hay truco, ¿eh?

Bueno, un poquito, sí. A ver, la caída libre ideal es un modelo, una simplificación. Muy útil, eso sí. Es el movimiento que haría un objeto si la única, y recalco, única, fuerza que actuara sobre él fuera la gravedad.

Nada de resistencia del aire, ni roces, ni nada. Solo la atracción pura del planeta.

Entendido. O sea, un mundo perfecto, sin aire. ¿Y cómo montamos ese escenario perfecto en nuestra simulación?

Pues es bastante fácil, la verdad. Hay que ir a los controles y buscar dos cosas. Primero, el selector que dice "Rozamiento con aire". Hay que ponerlo en cero, fuera aire.

Y segundo, la velocidad inicial. Asegurarnos de que esté desactivada o, bueno, en 0 m/s, que parta del reposo.

Con eso ya lo tienes. La simulación te muestra ese movimiento puro. La bolita que cae solo obedece a una cosa: la aceleración de la gravedad de ese planeta, la famosa $g$.

Y este movimiento tan... tan limpio se puede describir con un par de fórmulas clave que seguro que a muchos os suenan.

La primera es para la velocidad final, $v_f$. Se escribe así: $$ v_f = v_0 + gt $$

Eso es. A ver, leída sería $v_f$ es igual a $v_0$ más $g$ por $t$. Donde $v_0$, pues es la velocidad inicial, que si lo soltamos es cero, claro. $g$ es la aceleración de la gravedad y $t$ el tiempo.

Básicamente te dice cómo va aumentando la velocidad, segundo a segundo, por culpa de la gravedad.

Y la otra fórmula importante es para ver cuánto ha caído, el desplazamiento vertical. Lo llamamos $\Delta y$. La fórmula es: $$ \Delta y = v_0 t + \frac{1}{2}gt^2 $$

Exacto. Leída completa: $\Delta y$ es igual a $v_0$ por $t$ más $\frac{1}{2}$ de $g$ por $t$ al cuadrado. Fíjate que relaciona la distancia caída con el tiempo al cuadrado, y de nuevo con $v_0$ y $g$.

Pero lo bueno de la simulación no es solo ver las fórmulas escritas, es verlas en acción. Ves la bola acelerar, ¿no? Puedes poner los medidores y tomar datos de velocidad, de posición, y compruebas que los números encajan justo con lo que dicen las ecuaciones. Es una pasada, una verificación al instante.

Vale, eso si soltamos el objeto y ya está, desde el reposo. Pero, ¿qué pasa si le damos un empujoncito hacia abajo al empezar? Si usamos esa opción de velocidad inicial y le ponemos, no sé, 10 m/s hacia abajo. ¿Sigue siendo caída libre?

Porque ya no parte de cero.

Muy buena pregunta. Aquí es donde se pone realmente interesante. Y la respuesta corta es que sí, técnicamente sí sigue siendo caída libre.

¿Incluso con velocidad inicial? Pero, ¿por qué?

Porque la definición se basa en las fuerzas que actúan durante el movimiento. Una vez tú lo has lanzado, aunque ya lleve una velocidad inicial, si seguimos en nuestro mundo ideal sin aire, la única fuerza que actúa sobre él sigue siendo la gravedad, solo $g$. Así que su movimiento sigue estando gobernado únicamente por esa aceleración constante $g$.

Ah, vale. Lo entiendo. O sea, no es "dejar caer", sino "lanzar hacia abajo", pero la física después del lanzamiento es la misma.

El material que revisamos proponía un experimento muy chulo para verlo claro en la simulación.

Sí, una comparación directa. Es muy visual. Probad a hacer esto. Primero, Caso 1. Poned la Tierra, rozamiento cero, y soltáis una bola desde, digamos, 1000 metros, $v_0 = 0$.

Lanzad la simulación y activad gráficas y datos. Anotad cuánto tarda en llegar abajo y con qué velocidad final choca. Vale. Ahora, Caso 2. Reiniciad todo igual, misma altura 1000 metros, Tierra, rozamiento cero, pero ahora dadle una velocidad inicial hacia abajo, por ejemplo, 20 m/s.

Y volvéis a lanzar y anotáis el tiempo y la velocidad final.

A ver, la intuición me dice que en el segundo caso llegará antes al suelo y además llegará a más rápido, ¿no? Porque ya salía con ventaja.

Eh, exacto. Tu intuición es correcta. Y los datos de la simulación lo van a confirmar. Menos tiempo de caída y más velocidad al final en el caso 2.

Pero, y aquí está la clave de todo esto, si te fijas en cómo cambia la velocidad en cada instante, verás que la aceleración, el ritmo al que aumenta la velocidad, es exactamente el mismo en los dos casos.

Siempre es $g$, unos 9.8 m/s cada segundo en la Tierra. Ese empujón inicial cambia las velocidades, claro, pero no cambia cómo la gravedad las hace aumentar.

Entendido. Esa $g$ constante es la protagonista total en el caso ideal sin aire.

Y una forma genial de verla en acción son las gráficas.

Absolutamente. Las gráficas son como... como el lenguaje secreto de la física, pero hecho visible. Analicemos las dos que nos da la simulación en caída ideal, ¿vale?

Primero, la de altura frente al tiempo, la que se llama $y-t$. ¿Qué forma tiene?

Es una curva, ¿verdad? Como media parábola que empieza más plana y se va inclinando hacia abajo cada vez más rápido.

Justo eso, media parábola. Y esa forma no es casualidad, ¿eh? Viene directa de la ecuación que vimos antes, $\Delta y = v_0t + \frac{1}{2}gt^2$. Como la posición $\Delta y$ depende del tiempo al cuadrado, de $t^2$, pues la gráfica es una parábola.

Y que se haga más empinada, como dices, más vertical, significa que en cada segundo que pasa recorre más distancia que en el segundo anterior.

Claro, es la prueba visual de que está acelerando.

Exacto. Y ahora la otra gráfica importante, la de velocidad frente a tiempo, la $v-t$. En este caso ideal, sin rozamiento...

Esa es más fácil, es una línea recta que sube y sube con la misma inclinación todo el rato.

Correcto, una línea recta con pendiente positiva constante. Y esa forma, la línea recta en la gráfica $v-t$, es la firma de lo que llamamos un Movimiento Rectilíneo Uniformemente Acelerado, un MRUA.

O sea, un movimiento donde la aceleración no cambia, es constante. Y la pendiente de esa recta, su inclinación, ¿qué crees que representa?

Pues si la velocidad aumenta siempre al mismo ritmo, y ese ritmo es $g$... la pendiente tiene que ser $g$.

¡Bingo! La pendiente de la recta $v-t$ es exactamente el valor de la aceleración $g$. Como $g$ es constante en caída libre ideal, la pendiente es constante, y por eso es una recta.

Es genial poder ver estos patrones. Animamos a todo el mundo que nos escucha a que juegue con la simulación. Activad gráficas y datos, lanzad algo sin rozamiento y fijaos en esas formas: parábola en $y-t$, recta en $v-t$. Es muy clarificador.

Totalmente. Hasta ahora todo ha sido en ese mundo un poco de fantasía, sin aire. Pero claro, en el mundo real, el aire está ahí y frena las cosas. ¿Cómo cambia el juego cuando metemos el rozamiento en la simulación?

Pues cambia bastante, la verdad. Y el cambio fundamental afecta a la aceleración. Recuerda... en el caso ideal, la aceleración era constante, siempre $g$. Y la velocidad, pues en teoría, podría aumentar sin límite.

Vale.

Pero cuando activas el rozamiento con aire, aparece una fuerza nueva, la resistencia del aire. Y esta fuerza tiene dos características importantes: una, siempre va en contra del movimiento (si caes, ella tira para arriba) y dos, y esto es crucial, se hace más fuerte cuanto más rápido vas.

¡Ostras! A ver, entonces, tenemos la gravedad, que tira para abajo siempre igual. Y ahora una fuerza de rozamiento que tira para arriba, pero que cada vez tira más fuerte según vas más rápido.

Eso significa que la fuerza total que te empuja hacia abajo ya no es constante.

¡Exactamente! La fuerza neta, que es la resta entre la gravedad hacia abajo y el rozamiento hacia arriba, ya no es constante. Al principio, cuando empiezas a caer y vas despacio, el rozamiento es pequeño y la fuerza neta es casi $g$. Pero según coges velocidad, el rozamiento aumenta y la fuerza neta se va haciendo más pequeña.

Y si la fuerza neta disminuye... aquí entra Newton, ¿no? Su segunda ley, $F=ma$. Si la fuerza baja, la aceleración también tiene que bajar.

Precisamente. El objeto sigue ganando velocidad, sí, pero cada vez más despacio. Su aceleración ya no es constante como $g$, va disminuyendo poco a poco.

O sea, acelera cada vez menos.

Eso es. El material de referencia tenía una imagen muy buena comparando las gráficas $v-t$. La ideal era una recta perfecta. La que tiene rozamiento es una curva que empieza subiendo rápido, pero luego se va doblando, se va aplanando.

Entendido. Ya no es una línea recta porque la aceleración no es constante.

Y ese aplanamiento de la curva de velocidad nos lleva a otro concepto súper interesante: la velocidad límite, o velocidad terminal creo que también se llama. ¿Qué es eso?

Pues es justo la consecuencia de ese rozamiento que aumenta con la velocidad. Lo fascinante aquí es que llega un momento en que el objeto deja de acelerar por completo.

¿Cómo que deja de acelerar?

Sí, sí, piensa en las fuerzas: gravedad hacia abajo, constante; rozamiento hacia arriba, aumentando con la velocidad. Llega un punto en que la velocidad es tan alta que la fuerza de rozamiento hacia arriba se hace exactamente igual de grande que la fuerza de la gravedad hacia abajo.

Ah, se equilibran.

¡Exacto! Las dos fuerzas principales se anulan mutuamente. La fuerza neta sobre el objeto se vuelve... cero.

Cero. Y... si la fuerza neta es cero, la primera ley de Newton dice que si algo se mueve, sigue moviéndose a velocidad constante. La aceleración se hace cero.

Ahí lo tienes. El objeto ha llegado a su velocidad máxima posible en esas condiciones de aire, con esa forma, esa masa... ya no puede ir más rápido. A partir de ese momento, si sigue cayendo, lo hace a esa velocidad constante, la velocidad límite. Fin de la aceleración.

La simulación tiene una forma muy visual de pillar esto, ¿verdad? Con los vectores esos de colores.

Sí, es genial para verlo. Probad esto: poned un rozamiento alto para que pase rápido, y una altura grande, como 4000 metros, para que le dé tiempo.

Y muy importante, activad la casilla "Ver vectores". Vale. Al lanzar la bola, veréis una flecha amarilla hacia abajo, que es la velocidad, y una flecha roja hacia arriba, que es el rozamiento.

Y hay que fijarse en cómo cambia la flecha roja, ¿no?

Eso es. Veréis que mientras la amarilla (velocidad) crece, la roja (rozamiento) también crece. Y llegará un momento en que la flecha roja será igual de larga que la fuerza de gravedad que, aunque no se dibuja, sabemos que tira hacia abajo.

En ese preciso instante, la velocidad deja de aumentar, la flecha amarilla se queda quieta en su tamaño. Esa es la velocidad límite.

Qué bueno, verlo así ayuda un montón.

El material comentaba que, para simplificar, muchas simulaciones usan un modelo donde el rozamiento es proporcional a la velocidad, o sea, $Rozamiento = b \cdot v$, donde $b$ es un número que depende del aire, de la forma del objeto...

Y si además asumen que la masa es 1 kg, la fórmula para la velocidad límite, $v_t$, queda muy sencilla: $$ v_t = \frac{g}{b} $$

O sea, $v_t$ igual a $g$ partido por $b$.

Exacto. Cuanto mayor sea el rozamiento $b$ —por ejemplo, un paracaídas tiene una $b$ muy grande—, menor será la velocidad límite. Y esto es súper importante en la vida real, claro, desde paracaídas hasta cómo caen las gotas de lluvia.

Y para mirar todo esto con números, no solo con dibujitos, la simulación nos da la tabla de datos. El material decía que es como un "cuaderno de laboratorio digital". Me gusta la idea. ¿Qué podemos hacer con ella?

Pues es una herramienta súper potente, la verdad. Para el análisis cuantitativo, vamos. Cuando la activas, la simulación va anotando cada poquito tiempo, la altura exacta y la velocidad exacta del objeto. Es como tener el diario de viaje completo de la bola.

¿Y eso para qué nos sirve en la práctica, estudiando?

Uf, para muchas cosas. Primero, lo más obvio: verificar tus cálculos. Si resuelves un problema en papel, calculas el tiempo de caída, la velocidad final... puedes poner esas mismas condiciones en el simulador y ver si los números de la tabla coinciden con los tuyos. Es una forma genial de autocorregirte.

Vale, eso es útil.

Segundo, para analizar los números directamente. Puedes mirar la columna de velocidad y ver cuánto aumenta entre un segundo y el siguiente. Si estás en caída ideal, confirmarás que el aumento es siempre el mismo, es $g$. Si estás con rozamiento, verás que ese aumento se va haciendo cada vez más pequeño.

Hasta que se acerca a cero cuando llega a la velocidad límite, supongo.

Exacto. Ves numéricamente cómo la aceleración disminuye.

Y he visto que hay un botón que pone "Descargar CSV". ¿Eso qué es?

¡Ah, eso es genial! Te permite exportar todos esos datos de la tabla a un archivo `.csv`. Es un formato que puedes abrir con programas como Excel, Google Sheets o cualquier hoja de cálculo.

Así que si necesitas hacer gráficas más personalizadas para un trabajo, o un análisis más detallado, o guardar los resultados de varios experimentos para compararlos, pues te bajas el CSV y listo. Es muy práctico.

Excelente. Pues vamos a poner todo esto a prueba, ¿no? El material proponía un experimento que suena muy bien: intentar calcular la gravedad en Marte usando solo la simulación. Parece una misión de la NASA. ¿Cómo se hace?

Jaja, sí, suena potente, pero es un ejemplo perfecto de cómo usar la simulación como si fuera un experimento de verdad. Aquí es donde se pone realmente interesante.

A ver, los pasos serían estos. 1: Configuración marciana. En la simulación elegimos Marte como planeta, importantísimo. Rozamiento en cero y velocidad inicial 0 m/s. Queremos la caída libre ideal de Marte.

Vale. Marte, sin aire y soltando desde parado.

2: Puntos de control. Cogemos los dos medidores que tiene la simulación y los ponemos en dos alturas que conozcamos bien y que estén separadas. Por ejemplo, uno arriba, a 4000 metros, y otro más abajo a 2000 metros.

La distancia vertical entre ellos, $\Delta y$, es de 2000 metros. Anotamos eso.

Listo. Medidores colocados. $\Delta y = 2000$ m.

3: Lanzar y registrar. Le damos a iniciar. La bola empieza a caer. Tenemos que fijarnos en la velocidad que marca justo al pasar por el primer medidor. Esa será nuestra velocidad inicial del tramo, la llamamos $v_i$.

Y la velocidad al pasar por el segundo medidor, la velocidad final del tramo, $v_f$.

Vale, apuntamos $v_i$ y $v_f$ de los medidores.

4: La física al rescate. Hay una fórmula de cinemática súper útil que no necesita el tiempo. Es esta: $$ v_f^2 = v_i^2 + 2g\Delta y $$

A ver, la leo despacio: $v_f^2$ es igual a $v_i^2$ más 2 por $g$ por $\Delta y$. Fíjate que relaciona las dos velocidades que hemos medido ($v_i, v_f$), la distancia que conocemos ($\Delta y$) y la $g$ de Marte, que es lo que queremos encontrar.

Ah, claro, nuestra incógnita está ahí metida.

5: Despejar la $g$. Solo hay que reorganizar un poco esa fórmula para dejar la $g$ sola. Queda así: $$ g = \frac{v_f^2 - v_i^2}{2\Delta y} $$

La repito: $g$ es igual a ($v_f^2 - v_i^2$) todo eso dividido entre (2 por $\Delta y$).

Vale, tenemos la fórmula para calcular $g$.

6: El momento de la verdad. Cogemos los valores de $v_f$ y $v_i$ que medimos antes y el valor de $\Delta y$ (2000 metros), los metemos en la fórmula. Hacemos la cuenta con la calculadora y el resultado debería ser increíblemente cercano a 3.71 m/s².

¡Ostras! Que es justo el valor conocido de la gravedad en Marte.

Es alucinante. Sin movernos de la silla, con una simulación y sabiendo un poco de física, hemos medido la gravedad en otro planeta. Esto sí que demuestra lo potentes que son estas herramientas y entender los principios. ¡Imagina para planificar misiones espaciales de verdad!

Exacto. Es una demostración muy chula.

Bueno, estamos ya casi al final. Pero no podemos irnos sin mencionar, aunque sea rápido, al primo hermano de la caída libre: el tiro vertical. Están relacionados, ¿no?

¡Uf! Totalmente. Son las dos caras de la misma moneda, podríamos decir. En el tiro vertical, tú lanzas algo hacia arriba. La gravedad, que siempre tira hacia abajo, actúa como un freno, va quitándole velocidad.

Ajá, hasta que se para arriba del todo.

Exacto. Llega a una altura máxima y justo en ese instante, su velocidad es cero. ¿Y qué pasa justo después de ese instante?

Pues que empieza a caer.

Y esa caída, desde la altura máxima hasta abajo, es exactamente una caída libre. Una caída libre que empieza desde el reposo en esa altura máxima.

Claro, es la segunda mitad del viaje.

Si conectamos esto con una perspectiva más amplia, vemos que es la misma física, la misma $g$ constante tirando para abajo, la que gobierna todo. Primero frena la subida y luego acelera la bajada.

Por cierto, para quien le interese explorar más esto, en Aula Quest también hay una simulación específica para el tiro vertical, para verlo con todo detalle.

Genial saberlo. Pues sí que hemos cubierto terreno hoy, ¿eh? A ver, recapitulando rápido: hemos definido la caída libre ideal (solo gravedad, sin aire).

Hemos visto qué pasa si hay velocidad inicial (sigue siendo caída libre ideal si no hay roce). Hemos aprendido a leer las gráficas (parábola en $y-t$, recta en $v-t$).

Hemos visto la diferencia clave con el rozamiento real (aceleración disminuye). Hemos entendido qué es la velocidad límite (cuando roce = gravedad).

Hemos visto lo útil que es la tabla de datos (cuaderno digital). Y hasta hemos medido la gravedad en Marte. Entonces, ¿qué significa todo esto, con qué nos quedamos?

Pues yo diría que nos quedamos con dos ideas principales. Una, que tenemos un modelo ideal simplificado (la caída sin rozamiento) que nos ayuda a entender los principios básicos de forma muy clara.

Y dos, que herramientas como esta simulación son fantásticas porque nos permiten ir más allá del modelo ideal. Nos dejan ver cómo factores del mundo real, como el rozamiento del aire, cambian las cosas y nos llevan a fenómenos tan importantes como la velocidad límite.

Muy bien resumido. Y para dejar a nuestros oyentes de Aula Quest con algo para darle vueltas, una última reflexión que salía del material. Sabemos que el rozamiento del aire depende de la velocidad, pero también de la forma y el tamaño del objeto, ¿verdad?

Ajá.

Entonces, ¿cómo podría esto explicar eso que vemos todos los días, que una pluma y una bola de bolos caen de forma súper diferente en el aire, aunque la gravedad $g$ sea la misma para las dos?

Buena pregunta.

¿Y qué implicaciones tiene eso para la velocidad límite que pueden alcanzar cosas muy distintas? No sé, pensad en un globo aerostático enorme pero ligero, comparado con un perdigón pequeñito pero denso. ¿Quién tendrá mayor velocidad límite? ¿Por qué?

Ahí queda eso, para seguir pensando y, sobre todo, experimentando con la simulación.

Exacto. Muchísimas gracias a todos y todas en Aula Quest por habernos acompañado hoy. Os animamos un montón a que abráis la simulación, cambiéis cosas, probéis otros planetas, juguéis con el rozamiento... es la mejor forma de que todo esto se os quede grabado. Hasta la próxima exploración.

Primero: ¿Qué es la "caída libre" y cómo la representa este simulador interactivo?

La caída libre es el movimiento ideal de un objeto que se encuentra bajo la influencia exclusiva de la gravedad. Esto significa que no consideramos ninguna otra fuerza, como la resistencia del aire.

En este simulador de caída libre, puedes recrear una caída libre perfecta de una forma muy sencilla:

Asegúrate de que el selector de "Rozamiento con Aire" esté en "Cero".
Asegúrate de que la "Velocidad Inicial" esté desactivada (o en 0 m/s).

Al hacer esto, la única "regla" que sigue la bola es la aceleración de la gravedad 'g' del planeta que elijas. Este movimiento se describe con dos fórmulas clave que puedes verificar con nuestra simulación de caída libre:

$$v_f = v_0 + g \cdot t$$ $$\Delta y = v_0 \cdot t + \frac{1}{2} g \cdot t^2$$

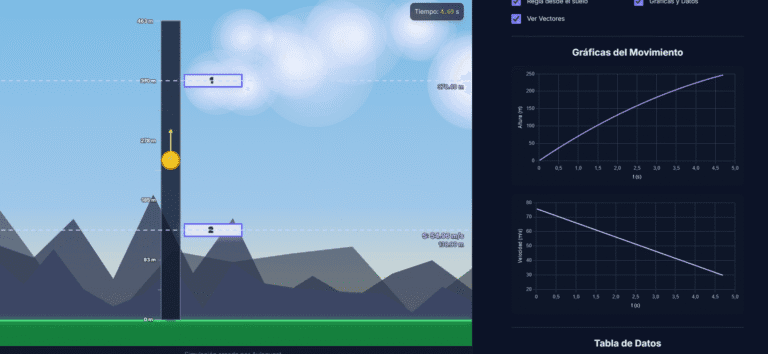
La simulación te permite visualizar esto directamente: ves la bola acelerar, mides su velocidad y posición con los medidores y compruebas los resultados en las gráficas y la tabla de datos.

¿Qué ocurre si añado una "Velocidad Inicial"? ¿Sigue siendo una caída libre interactiva?

¡Gran pregunta! Técnicamente, sí, sigue siendo un movimiento de caída libre siempre que el rozamiento sea cero, porque la gravedad sigue siendo la única fuerza que actúa sobre el objeto una vez lanzado.

Sin embargo, en lugar de "dejar caer" el objeto desde el reposo ($v_0 = 0$), lo que estás simulando en esta caída libre interactiva es un lanzamiento vertical hacia abajo. El objeto ya parte con una ventaja.

Experimento rápido en la simulación de caída libre:

Caso 1: Deja caer la bola desde 1000 m con velocidad inicial 0 m/s. Activa "Gráficas y Datos" y anota el tiempo total de caída y la velocidad final.
Caso 2: Reinicia y vuelve a lanzar desde 1000 m, pero esta vez activa la "Velocidad Inicial" y ajústala a 20 m/s.

Al comparar los datos de la tabla, verás que en el segundo caso, el objeto tarda menos tiempo en llegar al suelo y su velocidad final es mayor. Esto es porque empezó con un "empujón" inicial, pero la forma en que su velocidad aumentó cada segundo (su aceleración) fue exactamente la misma: 'g'.

¿Qué significan las formas de las gráficas del movimiento?

Las gráficas son la herramienta visual más poderosa para entender el movimiento. Para una caída libre ideal (sin rozamiento), nos cuentan una historia muy clara:

Gráfica Altura vs. Tiempo (y-t): Como puedes ver, tiene forma de media parábola. La curva se va haciendo cada vez más "vertical", lo que nos indica visualmente que el objeto recorre más metros en cada segundo que pasa. ¡Es la prueba gráfica de que está acelerando!
Gráfica Velocidad vs. Tiempo (v-t): Es una línea recta perfecta con pendiente positiva. Esto se debe a que, por convenio, consideramos la velocidad de caída como positiva. La pendiente (inclinación) de esta recta es, ni más ni menos, que el valor de la aceleración 'g'.
Gráfica Aceleración vs. Tiempo (a-t): Es una línea horizontal constante en +9.8 m/s². Usamos este valor porque es la aceleración de la gravedad promedio en la superficie de la Tierra. Al tomar la dirección de caída como positiva, la aceleración es constante y positiva.

Activa "Gráficas y Datos" en el simulador de caída libre, realiza un lanzamiento sin rozamiento y comprueba que obtienes estas mismas formas.

¿Qué diferencia hay entre la caída ideal y la caída con rozamiento en este simulador?

La diferencia clave es la aceleración.

Caída Ideal (Sin Rozamiento): La única fuerza es la gravedad, por lo que la aceleración es constante e igual a 'g'. La velocidad aumenta sin fin (teóricamente).
Caída con Rozamiento: Aparece la fuerza del aire, que se opone al movimiento. Esto hace que la aceleración neta disminuya a medida que el objeto cae más rápido, hasta que eventualmente se hace cero.

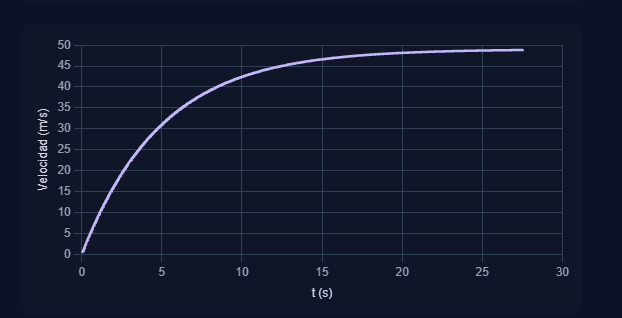
Gráfica de velocidad en caída con rozamiento (curva asintótica).

La velocidad con rozamiento tiende a un valor máximo constante: la velocidad límite.

Este fenómeno ocurre porque la fuerza de rozamiento ($F_r$) aumenta con la velocidad. Se alcanza un equilibrio cuando la fuerza de rozamiento iguala a la fuerza de la gravedad ($F_g$).

$$F_g = F_r \implies mg = b \cdot v_t$$

En este simulador interactivo de caída libre asumimos una masa $m=1$ kg y un rozamiento lineal con la velocidad ($F_r = b \cdot v$), por lo que la velocidad límite es $v_t = g/b$.

¿Qué es la "velocidad límite" y cómo la explican los vectores en la simulación?

La velocidad límite (o terminal) es la máxima velocidad que un objeto puede alcanzar en una caída con rozamiento. Se produce cuando la fuerza de rozamiento hacia arriba se iguala en magnitud a la fuerza de la gravedad hacia abajo.

En ese punto, la fuerza neta sobre el objeto es cero, y según la Primera Ley de Newton, la aceleración es cero. Por tanto, el objeto deja de acelerar y su velocidad se mantiene constante.

Usa los vectores en este simulador de caída libre para entenderlo:

Selecciona un rozamiento "Alto" y una altura grande (ej. 4000 m).
Activa la opción "Ver Vectores".
Al lanzar, verás el vector de velocidad (amarillo) apuntando hacia abajo, y el de rozamiento (rojo) apuntando hacia arriba.
Observa cómo, a medida que el objeto gana velocidad, el vector rojo crece hasta igualar la fuerza de la gravedad. En ese instante, la velocidad se estabiliza. ¡Has alcanzado la velocidad límite!

¿Cómo puedo usar la "Tabla de Datos" de esta simulación de caída libre para mis estudios?

La tabla de datos de nuestro simulador interactivo es tu cuaderno de laboratorio digital. Al activar "Gráficas y Datos", la simulación registra el tiempo, la altura y la velocidad en intervalos regulares, dándote una fotografía numérica del movimiento.

Es extremadamente útil para:

Verificar Cálculos: Compara los resultados de tus problemas con los datos precisos de esta caída libre interactiva.
Análisis Cuantitativo: Observa cuánto aumenta la velocidad cada segundo. En una caída ideal, verás que este aumento es constante (es la aceleración 'g').
Exportar para Análisis Avanzado: El botón "Descargar CSV" te permite guardar los datos para abrirlos en Excel o Google Sheets y crear tus propias gráficas para informes o proyectos.

Propuesta de trabajo: Calcular 'g' en Marte con el simulador de caída libre

Podemos usar los medidores de esta simulación interactiva de caída libre para realizar un experimento y calcular la gravedad en Marte.

Configura el entorno: Selecciona "Marte", rozamiento "Cero" y velocidad inicial 0.
Coloca los medidores: Arrastra los medidores a dos alturas conocidas, por ejemplo, a 4000 m y a 2000 m. La distancia entre ellos ($\Delta y$) es de 2000 m.
Lanza y registra datos: Inicia la simulación y anota la velocidad en el primer medidor ($v_i$) y en el segundo ($v_f$).
Aplica la física: Usa la ecuación de cinemática que no depende del tiempo:

$$v_f^2 = v_i^2 + 2 \cdot g \cdot \Delta y$$

Despejando la aceleración (g), obtenemos:

$$g = \frac{v_f^2 - v_i^2}{2 \cdot \Delta y}$$

Sustituye los valores que obtuviste. El resultado debería ser muy cercano a 3.71 m/s², ¡la gravedad de Marte!

¿Y si quiero explorar el Tiro vertical?

¡Excelente curiosidad! El lanzamiento vertical hacia arriba es el "movimiento hermano" de la caída libre. En lugar de empezar desde el reposo y caer, le das al objeto una velocidad inicial hacia arriba. El objeto subirá, frenando por la gravedad, hasta alcanzar una altura máxima, y luego caerá exactamente igual que en esta simulación.

Hemos creado una simulación específica para analizar este movimiento en detalle, donde podrás controlar la velocidad de lanzamiento y ver cómo alcanza su punto más alto.

Explorar el Simulador de Tiro Vertical

Historias fascinantes en el blog de Aulaquest

👨‍🚀 Cuando la Física se Lanza al Vacío

Un hombre. 39 kilómetros de altura. Y las mismas ecuaciones que acabas de usar en esta simulación. Descubre cómo Felix Baumgartner convirtió la caída libre en una lección de física a escala planetaria:

👉 Descubre el salto más loco — y más preciso — de la historia

Blog

Quiz Interactivo: Caída Libre

Quiz de Caída Libre

Demuestra que dominas la gravedad, la aceleración y los efectos del rozamiento.

Elige un nivel de dificultad:

Zona de Actividades de tu Profesor

Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.

Widget de Contacto

Simulaciones en fisica

Física