Simulador de Tiro Vertical
📎 Código para incrustar
¿Eres profe, divulgador o webmaster?
Puedes incrustar esta simulación en tu web o blog sin problema.
Solo pedimos dos cosas básicas:
- ✅ Que cites la fuente: AulaQuest.com
- 🚫 Que no la uses con fines comerciales
Este es el código que puedes copiar:
<iframe
src="https://sim.aulaquest.com/fisica/lanzamiento-vertical.html"
width="100%"
height="560"
style="border: 1px solid #ccc; border-radius: 8px;"
allowfullscreen
title="Simulador de tiro vertical"></iframe>
Simulador de tiro vertical
Iniciando simulación...
¿Qué es el "tiro vertical" y cómo funciona este simulador interactivo?
El tiro o lanzamiento vertical es un movimiento donde un objeto es lanzado hacia arriba, en contra de la gravedad. La gravedad (g) actúa como un "freno", disminuyendo la velocidad del objeto hasta que se detiene momentáneamente en su punto más alto, para luego hacerlo caer.
Uso del Laboratorio Interactivo:
Este laboratorio de tiro vertical interactivo te permite analizar este fenómeno al detalle. Para un lanzamiento ideal:
- Ajusta la "Velocidad Inicial (v₀)" con la que quieres lanzar el objeto.
- Asegúrate de que el "Rozamiento con Aire" esté en "Cero".
El movimiento se rige por las mismas ecuaciones de la cinemática. La velocidad inicial (v₀) es positiva (hacia arriba) y la aceleración de la gravedad (g) es negativa.
vf = v₀ - g · t
yf = y₀ + v₀ · t - 1/2 g · t²
Nuestro simulador de tiro vertical aplica estas fórmulas para mostrarte la trayectoria, la altura máxima y las velocidades en cualquier punto.
¿Cómo se alcanza la "Altura Máxima" en este lanzamiento vertical interactivo?
La altura máxima (Hmax) es el punto más importante del tiro vertical. Se alcanza en el preciso instante en que la velocidad del objeto se vuelve cero (v_f = 0). A partir de ahí, la gravedad "gana la batalla" y el objeto empieza a caer.
Podemos calcularla usando esta fórmula, que se deduce de las anteriores:
H_max = y₀ + v₀² / (2g)
Compruébalo en la simulación:
- Lanza un objeto con cualquier velocidad inicial (ej. 50 m/s) desde el suelo (y₀ = 0) y sin rozamiento.
- El simulador marcará automáticamente la "H. max" alcanzada, un detalle visual muy útil para tus análisis.
- Activa "Gráficas y Datos". Observa en la gráfica v-t el punto exacto donde la línea cruza el eje horizontal (velocidad = 0). El tiempo en ese punto es el tiempo que tardó en subir.
¿Cómo se ve la gráfica de Altura-Tiempo (y-t) en un tiro vertical ideal?
La gráfica de Altura-Tiempo (y-t) muestra la posición vertical (altura) del objeto a lo largo del tiempo. Para un tiro vertical ideal (sin rozamiento) con una velocidad inicial de v₀=20 m/s (g=9.8 m/s²), tiene la forma de una parábola invertida.
Gráfica Altura-Tiempo (y-t)
Muestra la altura del objeto a lo largo del tiempo, formando una parábola simétrica.
- Inicio (izquierda): La pendiente de la curva es positiva y alta (+20 m/s), indicando que el objeto sube rápidamente.
- Punto más alto (vértice de la parábola): La pendiente se vuelve cero. Esto representa el instante en que el objeto alcanza su altura máxima y su velocidad vertical es nula, justo antes de empezar a caer.
- Caída (derecha): La pendiente se vuelve negativa y su valor absoluto aumenta. Esto significa que el objeto está cayendo, y su velocidad hacia abajo se incrementa.
- Simetría: En un tiro vertical ideal, la parábola es simétrica. El tiempo que tarda en subir a una altura es el mismo que tarda en bajar desde esa altura.
¿Cómo se interpreta la gráfica de Velocidad-Tiempo (v-t) en un tiro vertical ideal?
La gráfica de Velocidad-Tiempo (v-t) es crucial para entender cómo la velocidad cambia a lo largo del tiempo bajo la influencia constante de la gravedad. Para un tiro vertical ideal (v₀=20 m/s, g=9.8 m/s²), es una línea recta con pendiente negativa constante.
Gráfica Velocidad-Tiempo (v-t)
Muestra la velocidad vertical del objeto, que decrece linealmente.
- Velocidad inicial: La línea comienza en el eje Y en un valor positivo (ej. +20 m/s), que es la velocidad de lanzamiento inicial hacia arriba.
- Pendiente constante y negativa: La línea tiene una pendiente constante y negativa. Esta pendiente representa la aceleración del objeto, que es la aceleración de la gravedad (–9.8 m/s²) y actúa de manera constante.
- Cruce por el eje X: El punto donde la línea cruza el eje del tiempo (eje X) indica el instante en que la velocidad es cero. Este es el momento exacto en que el objeto alcanza su altura máxima.
- Velocidades negativas: Después de cruzar el eje X, la línea continúa hacia valores negativos de velocidad. Esto significa que el objeto está cayendo, y su velocidad se vuelve negativa (hacia abajo) y su magnitud (rapidez) aumenta.
¿Cómo se representa la Velocidad Límite en una gráfica (v-t) con rozamiento?
Cuando consideramos el rozamiento con el aire, el movimiento de caída no es una aceleración constante. La fuerza de rozamiento se opone al movimiento y aumenta con la velocidad. Eventualmente, la fuerza de rozamiento iguala a la fuerza de gravedad, y la aceleración se vuelve cero. En ese punto, el objeto alcanza una velocidad constante llamada velocidad límite (v_límite).
Gráfica Velocidad-Tiempo (v-t) con Rozamiento
Muestra la velocidad de un objeto cayendo con rozamiento, aproximándose a una velocidad límite.
- Inicio de la caída: Si el objeto se deja caer (velocidad inicial cero), su velocidad comienza a aumentar debido a la gravedad.
- Efecto del rozamiento: A medida que la velocidad aumenta, la fuerza de rozamiento del aire también aumenta, reduciendo la aceleración neta del objeto.
- Curva de aproximación: La gráfica muestra una curva que se aplana con el tiempo, indicando que la aceleración disminuye.
- Velocidad límite: La curva se acerca asintóticamente (nunca la cruza, solo se aproxima) a una línea horizontal, que representa la velocidad límite. En este punto, la fuerza de rozamiento es igual y opuesta a la fuerza de gravedad, y la velocidad es constante.
- La fórmula para la velocidad límite es:v_límite = mg / bdonde 'm' es la masa, 'g' la gravedad y 'b' el coeficiente de rozamiento.
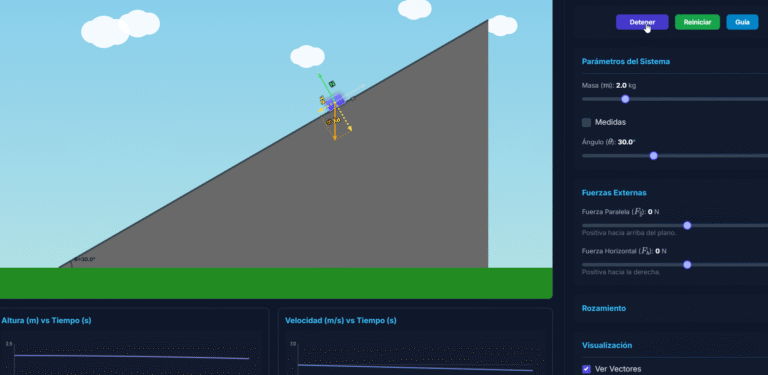
¿Cómo interpreto los vectores de velocidad y rozamiento?
Los vectores te dan una visión instantánea de las fuerzas y el movimiento. Es crucial no confundir el vector de rozamiento con el de la gravedad (g) (que no se dibuja, pero siempre apunta hacia abajo).
- Subida: El objeto sube, el rozamiento (rojo) y la gravedad frenan.
- Altura Máxima: La velocidad (amarillo) y el rozamiento (rojo) son cero. Solo actúa la gravedad.
- Bajada: La gravedad acelera el objeto y el rozamiento (rojo) se opone al movimiento, apuntando hacia arriba.
La Velocidad Límite (v_límite) (con rozamiento):
Durante la bajada, el rozamiento rojo crece. Si la caída es suficientemente larga, el rozamiento igualará a la gravedad, alcanzando la velocidad límite:
F_gravedad = F_rozamiento ⟹ mg = b · v_límite
En ese instante, la fuerza neta es cero y la aceleración también. La velocidad deja de aumentar. Despejando de esta relación, obtenemos la velocidad límite (incluyendo la masa 'm'):
v_límite = mg / b
Recuerda que estas ecuaciones son válidas solo cuando existe rozamiento con el aire. Puedes añadirlo para un análisis mas completo.
¿Cómo puedo simular escenarios realistas con las alturas inicial y objetivo?
Los controles de "Altura Inicial" y "Altura Objetivo" convierten este laboratorio en una herramienta muy versátil. Mira estos ejemplos:
- Lanzar desde un edificio:
- Lanzar para alcanzar una ventana:
- Lanzamiento en terreno irregular:
Fija la "Altura Inicial" en 50 m y la "Altura Objetivo" en 0 m para simular el lanzamiento de una pelota desde un balcón hasta la calle.
Fija la "Altura Inicial" en 0 m y la "Altura Objetivo" en 20 m para calcular la velocidad mínima necesaria.
Simula un lanzamiento desde una colina (ej. Inicial = 100 m) hasta un valle (ej. Objetivo = 30 m).
¡Dato clave! Cuando las alturas inicial y final son diferentes, el movimiento deja de ser simétrico. El tiempo de subida no será igual al tiempo de bajada.
¿Para qué sirve la "Tabla de Datos" y cómo puedo usarla?
La tabla de datos es tu cuaderno de laboratorio digital. Al activar "Gráficas y Datos", el simulador registra el tiempo, la altura y la velocidad en intervalos regulares. Es fundamental para:
- Verificar Cálculos:
- Análisis Detallado:
- Exportar para tus Proyectos:
Resuelve un problema en papel y compara tus resultados con los de la tabla para ver si son correctos.
Observa numéricamente el instante exacto en que la velocidad es cero (altura máxima).
Con el botón "Descargar CSV", puedes guardar los datos y usarlos en Excel o Google Sheets.
Propuesta de trabajo: Usar los medidores para comprobar la simetría
Los medidores móviles son perfectos para realizar experimentos. Sigue estos pasos para demostrar una propiedad clave del movimiento ideal:
- Configura: Selecciona "Rozamiento Cero", "Altura Inicial" 0 m y "Altura Objetivo" 0 m. Lanza con v₀=100 m/s.
- Coloca: Arrastra un medidor a una altura intermedia (ej. 200 m).
- Lanza: Inicia la simulación. El objeto pasará por el medidor subiendo y bajando.
Conclusión:
El medidor mostrará "S:" (velocidad de subida) y "B:" (velocidad de bajada) con valores idénticos. Esto es simetría y conservación de energía. ¡Si añades rozamiento "Medio", verás cómo la velocidad de bajada se reduce!
¿Y si quiero explorar solo la CAÍDA del objeto?
Si tu interés se centra exclusivamente en la segunda parte del viaje, cuando el objeto solo cae bajo el efecto de la gravedad, te recomendamos nuestro otro laboratorio especializado.
Hemos creado una simulación específica para analizar la **caída libre desde el reposo**, que es el complemento perfecto de esta herramienta.
Explorar el Simulador de Caída LibreQuiz del Simulador de Tiro Vertical
Pon a prueba tu comprensión del movimiento contra la gravedad. ¿Listo para el despegue?
Pregunta 1 de 10
Puntuación: 0
¡Desafío completado!
Tu puntuación final:
Análisis de Rendimiento
Zona de Actividades de tu Profesor
Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.
¿Tu última clase con la simulación fue un éxito?
Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Crear una actividad es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.
- 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
- 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
- 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
*Esto es solo para profes. Si lo eres, pide tu acceso.
Acceso Restringido
Este contenido de la Guía Docente solo está disponible para profesores registrados en Aulaquest.
Guía para el Docente
Simulación: Tiro Vertical
Esta guía se centra en el uso de la simulación de Tiro Vertical como una herramienta de indagación. Asumiendo que los estudiantes ya conocen las bases del MRUA, nos enfocaremos en conectar los conceptos abstractos (gravedad como aceleración constante) con sus representaciones visuales (gráficas y-t, v-t) y las consecuencias energéticas del rozamiento con el aire.
Objetivos de Aprendizaje
-
(Competencia STEM) Relacionar las gráficas de movimiento (
y-t,v-t) con el movimiento físico real del objeto (altura máxima, velocidad cero, aceleración constante). - (Competencia Digital) Verificar experimentalmente la simetría del movimiento ideal (conservación de energía) y la asimetría del movimiento real (disipación por rozamiento) usando la tabla de datos y los medidores.
-
(Competencia en Conciencia) Diferenciar conceptualmente entre velocidad (vector) y rapidez (escalar), e interpretar el significado físico de
v = 0en la altura máxima. -
Analizar cualitativa y cuantitativamente cómo el rozamiento del aire y el valor de
g(en diferentes planetas) afectan la altura máxima y el tiempo de vuelo.
Conecta con Aulaquest: Podquest
Anima a tus alumnos a escuchar el Podquest de Tiro Vertical mientras usan la simulación. El audio les guiará sobre qué observar (ej. "fíjate en la gráfica de velocidad, ¿cuándo cruza el cero?") mientras lo experimentan en tiempo real. Es la combinación perfecta, todo en la misma pantalla.
Por defecto, la simulación se inicia en modo de Exploración Libre. Piensa en esto como una "caja de arena" (sandbox) científica. Anima a los alumnos a "jugar" y ver qué pasa antes de imponer las leyes.
La interfaz te permite un control total sobre el lanzamiento. Estos son los controles principales:
Parámetros Controlables
- Velocidad Inicial (v0): Ajusta la velocidad (positiva o negativa) con la que se lanza el objeto.
- Altura Inicial (y0): Fija la altura desde la que se realiza el lanzamiento (ej. desde el suelo
y0=0o desde un edificioy0=50m). - Altura Objetivo (yobj): Establece una "meta" (línea verde) para resolver problemas específicos (ej. calcular el tiempo para llegar a
yobj=20m). - Lugar (Planeta): Permite cambiar la aceleración de la gravedad (
g) seleccionando Tierra 🌍, Luna 🌕, Marte 🪐, Júpiter ♃ o Venus ♀️. - Rozamiento con Aire (b): Controla la intensidad de la fricción (Cero, Medio, Alto).
- Escala de Altura: Ajusta el zoom vertical de la simulación para lanzamientos muy altos.
Toggles de Visualización
- Gráficas y Datos: Muestra/Oculta las gráficas (y-t, v-t) y la tabla de datos exportable (CSV).
- Ver Vectores: Muestra/Oculta los vectores de velocidad (amarillo) y rozamiento (rojo).
- Mostrar Altura/Tiempo: Muestra/Oculta los medidores en tiempo real.
- Regla desde el suelo: Muestra/Oculta la regla vertical.
- Ver Información de la Simu: Muestra/Oculta la guía de ayuda rápida.
Tu Primera Simulación (en 60s)
- Fija
v0 = 50 m/s,y0 = 0 myRozamiento = Ceroen laTierra 🌍. - Pulsa "Lanzar". Observa cómo la bola sube y cae. Fíjate en el valor de "Hmax".
- Activa "Gráficas y Datos". Observa la parábola de posición (y-t) y la línea recta de velocidad (v-t).
- Pulsa "Reiniciar". Ahora, cambia
Lugar = Luna 🌕. - Vuelve a lanzar. Compara: ¿La "Hmax" es mucho mayor? ¿Por qué la gráfica (y-t) es más ancha? (Pista:
ges menor). - Reinicia. Vuelve a
Tierra 🌍y ponRozamiento = Alto. Lanza y compara con el primer lanzamiento.
Conecta con Aulaquest: Presets y Personalización
¿Quieres que todos tus alumnos trabajen con la misma simulación? Configura las condiciones iniciales (por ejemplo, v0=30 m/s, Lugar = Marte 🪐, y0=100m) y genera un "Preset". Comparte la URL y tus alumnos verán exactamente tu configuración.
Además, puedes personalizar aún más la experiencia, por ejemplo, bloqueando el control de rozamiento para enfocar la lección solo en el MRUA ideal.
1. Hipótesis (¡El momento clave!)
"Vamos a poner el Rozamiento = Cero y lanzar desde el suelo (y0 = 0). Si lanzamos una pelota a 80 m/s:
1. ¿A qué velocidad volverá a chocar contra el suelo?
2. Si colocamos un medidor a 100m de altura, ¿qué velocidad marcará al subir? ¿Y al bajar? ¿Serán iguales?"
El Convenio de Signos (¡Importante!)
Recuerda a tus alumnos el convenio de signos que usa la simulación (y la física estándar):
- El eje Y es positivo hacia arriba. El suelo es
y=0. - La velocidad (v) es positiva (+) si el objeto sube y negativa (-) si el objeto baja.
- La aceleración de la gravedad (g) siempre apunta hacia abajo, por lo que es siempre negativa (ej.
g = -9.81 m/s2en la Tierra).
2. Experimentación (Simetría y Conservación de E)
Pide a los alumnos que sigan estos pasos:
- Pulsa "Reiniciar". Fija
v0 = 80 m/s,y0 = 0 myRozamiento = Cero. - Activa los "Medidores Móviles".
- Arrastra uno de los medidores hasta la marca de
H = 100 m. - Pulsa "Lanzar".
- Observa los valores que reporta el medidor en "S:" (Subida) y "B:" (Bajada).
3. Análisis y Conclusión
Guía la discusión para que concluyan:
- Los valores de "S:" y "B:" en el medidor son idénticos (ej. 60.8 m/s).
- Explicación (Energía): Esto demuestra la Conservación de la Energía Mecánica. A una misma altura (misma Energía Potencial), la Energía Cinética (y por tanto la rapidez) debe ser la misma, tanto al subir como al bajar.
- Pídeles que miren la gráfica. La parábola (y-t) es perfectamente simétrica.
- Si miran la tabla de datos, el tiempo de subida es exactamente igual al tiempo de bajada.
vf = v0 - g · t
yf = y0 + v0 · t - ½ g · t2
(Recuerda:
g en la Tierra es 9.81 m/s², pero cambia en otros planetas)¡Crea tus propias Actividades!
¡Esto es solo el principio! Con la herramienta "Actividades" de Aulaquest puedes crear ejercicios o grupos de ejercicios y tareas directamente asociados a esta simulación.
Por ejemplo, diseña un ejercicio donde los alumnos deban calcular la v0 necesaria para alcanzar una Hmax específica, o una tabla para rellenar con los tiempos y velocidades en diferentes alturas.
No necesitan registrarse, solo les das el código de la actividad y podrás ver sus resultados en directo en tu panel de control, ¡listo para seguimiento inmediato!
1. Hipótesis
"Ahora, ¿qué pasa si activamos el Rozamiento = Medio y repetimos el experimento anterior?
1. ¿La altura máxima será mayor o menor?
2. En el medidor a 100m, ¿la velocidad de bajada 'B:' será igual, mayor o menor que la de subida 'S:'?"
2. Experimentación (Disipación de Energía)
Pide a los alumnos que repitan el experimento anterior, pero con una sola diferencia:
- Pulsa "Reiniciar". Fija
v0 = 80 m/s,y0 = 0 myRozamiento = Medio. - Arrastra el medidor a
H = 100 m. - Pulsa "Lanzar" y observa atentamente los valores del medidor y la
Hmax.
3. Análisis y Conclusión
- La
Hmaxes significativamente menor. - En el medidor, la velocidad de bajada "B:" es menor que la velocidad de subida "S:".
- Explicación (Energía): El rozamiento es una fuerza no conservativa que disipa energía (en forma de calor).
Wr = ΔEmec.- Al subir,
gyFr(fuerza de rozamiento) frenan al objeto, por eso llega menos alto. - Al bajar,
gacelera peroFrfrena. La aceleración neta es menor queg. Por eso la gráfica v-t real (Gráfica 2) tiene una pendiente menos pronunciada al bajar y se curva hasta unavlímite(velocidad límite).
- Al subir,
- El tiempo de bajada es mayor que el tiempo de subida (porque la aceleración de bajada es menor).
Fgravedad = Frozamiento ⟹ mg = b · vlímite
(Para esta simulación, asumimos que la masa m = 1 kg, por lo que vlímite = g / b)
Conecta con Aulaquest: Quiz
Anima a tus estudiantes a ir a la pestaña Quiz: Cinemática y Tiro Vertical para poner a prueba su comprensión. Al finalizar, recibirán una autoevaluación que resalta sus puntos fuertes y las áreas que necesitan reforzar (ej. "Dominas el MRUA ideal", "Debes repasar el efecto del rozamiento").
Fomenta el Debate en Clase
Usa la simulación de Aulaquest para crear discusiones profundas que fomenten el pensamiento crítico. Lanza estas preguntas a la clase, pide que argumenten y defiendan su postura, y luego usad la simulación para encontrar la respuesta.
Pregunta: "Un paracaidista salta de un avión (v0 ≈ 0). Al principio, la gravedad (g) tira de él. La fuerza de rozamiento (Fr) aumenta con la velocidad. ¿Qué le pasa a su aceleración? ¿Acelera para siempre? ¿Qué pasa cuando abre el paracaídas?"
(Consejo: ¡Simuladlo! Fija v0 = 0 m/s, y0 = 2000 m, Lugar = Tierra 🌍 y Rozamiento = Medio. Lanza y mira la Gráfica 2 (v-t Real) para ver cómo la velocidad se estabiliza en la vlímite. Luego, simula 'abrir el paracaídas' reiniciando con Rozamiento = Alto. ¿Qué pasa con la vlímite ahora?)
Pregunta: "En la Luna, un astronauta soltó un martillo y una pluma, y cayeron a la vez. ¿Por qué en la Tierra no pasa eso? ¿Qué dos controles de la simulación tendrías que ajustar para simular el experimento del Apolo 15?"
(Consejo: Pide a los alumnos que seleccionen Lugar = Luna 🌕 y Rozamiento = Cero. ¡La simulación de Aulaquest replicará el famoso experimento!)
Pregunta: "Imagina que estás en Marte 🪐. Tienes que lanzar una pelota y hacer que alcance *exactamente* Hmax = 150 m. ¿Con qué v0 (Velocidad Inicial) tendrías que lanzarla? ¿Y si activas el Rozamiento = Medio, tendrías que lanzar con más o menos velocidad que antes para alcanzar los mismos 150m?"
(Consejo: Pide a los alumnos que seleccionen Lugar = Marte 🪐 (g=3.71 m/s²) y Rozamiento = Cero. Pueden calcular la v0 ideal (v0 = √(2·g·h) ≈ 33.3 m/s) y luego usar la simulación para comprobarlo. ¡Después, que intenten 'ganar' el concurso con el rozamiento activado! Verán que necesitan *mucha más* velocidad inicial.)
Consejos para el Docente (Herramientas PRO)
- Resolver Problemas (Altura Objetivo): Esta es la herramienta clave para problemas de libro no simétricos.
Ejemplo: "Calcula el tiempo de vuelo de un objeto lanzado desdey0=50mque debe aterrizar enyobj=20m". Los alumnos pueden calcularlo en papel y luego comprobarlo en la simulación fijandoAltura Inicial = 50yAltura Objetivo = 20. - Registro de Datos (CSV): El botón "Añadir Datos a la Tabla" es el cuaderno de laboratorio digital. Anima a tus alumnos a ser metódicos, recoger datos y luego pulsar "Exportar CSV". Analizar esos datos en Excel o Google Sheets es una competencia digital (LOMLOE) de primer nivel. Pídeles que grafiquen
vvst(sin rozamiento) y calculen la pendiente (¡debería ser-g!).
Valores de Gravedad (g) en la Simulación
Estos son los valores de aceleración gravitacional (g) que utiliza el simulador para cada planeta (en m/s2):
- Tierra 🌍: 9.81 m/s2
- Luna 🌕: 1.62 m/s2
- Marte 🪐: 3.71 m/s2
- Júpiter ♃: 24.79 m/s2
- Venus ♀️: 8.87 m/s2
Simulaciones en Física
¿CUÁL SERÁ TU PRÓXIMO DESCUBRIMIENTO?
¡Gran trabajo con esta simulación! Ahora puedes ampliar tus horizontes en otras áreas del conocimiento. ¿Por dónde quieres seguir?