Simulador de MRU y MRUA
🚗 Laboratorio virtual de MRU y MRUA
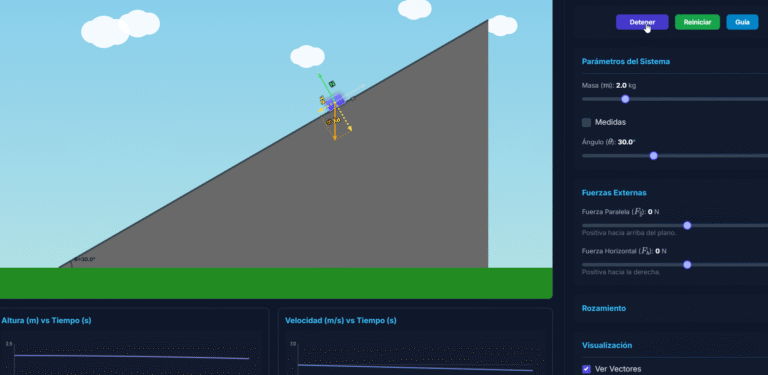
Explora el Movimiento Rectilíneo Uniforme y el Movimiento Rectilíneo Uniformemente Acelerado con este laboratorio virtual de cinemática
Controla parámetros como la posición inicial (x₀), la velocidad inicial (v₀), la aceleración (a) y la distancia total del escenario, para ver en tiempo real cómo evoluciona el movimiento. .
×
📎 Código para incrustar
¿Eres profe, divulgador o webmaster?
Puedes incrustar esta simulación en tu web o blog sin problema.
Solo pedimos dos cosas básicas:
- ✅ Que cites la fuente: AulaQuest.com
- 🚫 Que no la uses con fines comerciales
Este es el código que puedes copiar:
<iframe
src="https://sim.aulaquest.com/fisica/mru-mrua.html"
width="100%"
height="560"
style="border: 1px solid #ccc; border-radius: 8px;"
allowfullscreen
title="Simulador de MRU y MRUA"></iframe>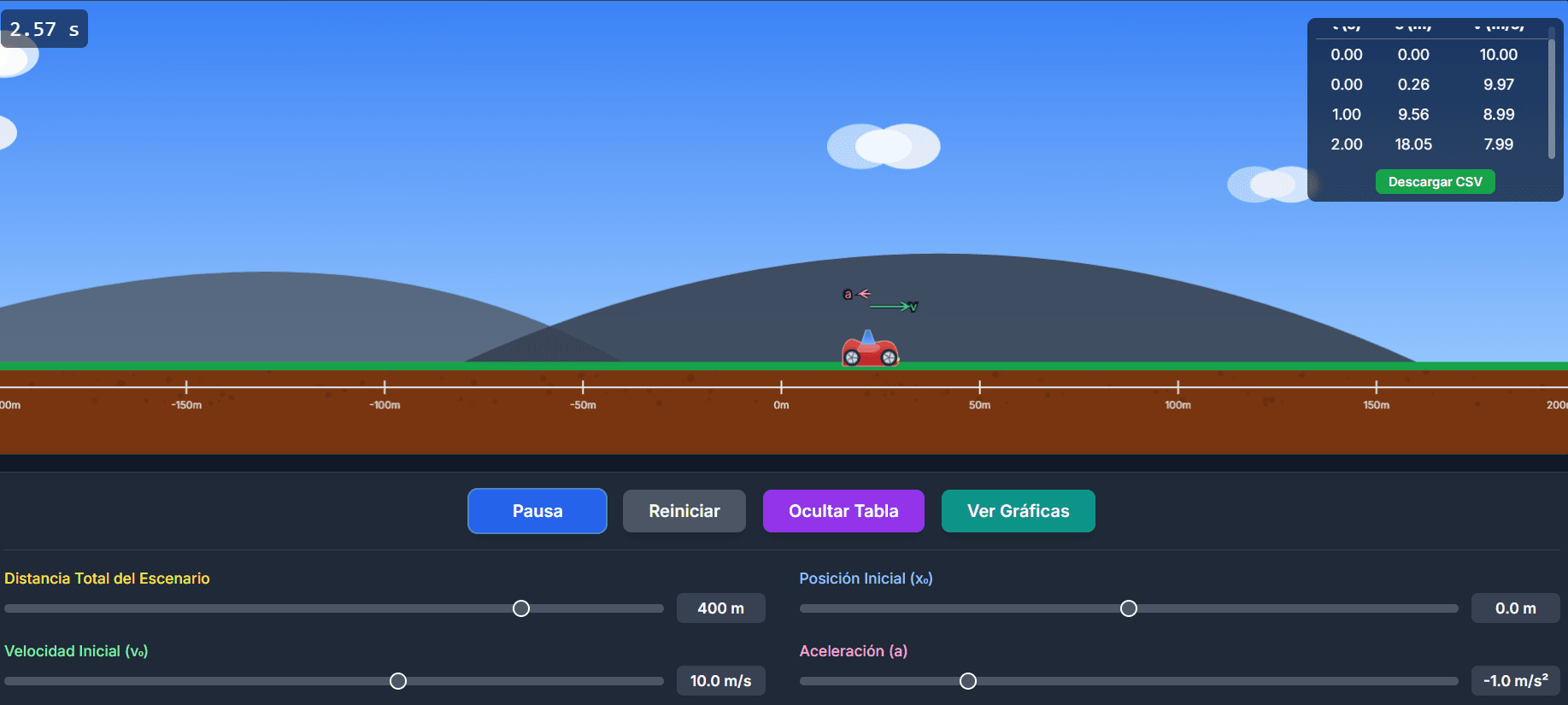
AulaQuest
Iniciando simulación...
Cinemática MRU vs MRUA
Hola a todos los exploradores del conocimiento en Aula Quest. Bienvenidos a una nueva inmersión profunda. Hoy vamos a meternos de lleno con la cinemática, que es el estudio del movimiento.
Y nos vamos a centrar en dos conceptos clave: el Movimiento Rectilíneo Uniforme (el MRU) y el Movimiento Rectilíneo Uniformemente Acelerado (o MRUA).
Tenemos aquí nuestros apuntes y, bueno, para quienes nos seguís desde Aula Quest, tenéis ahí ese simulador interactivo que es fantástico.
La idea hoy es entender bien qué es cada uno, cómo se diferencian y, sobre todo, cómo esa simulación nos ayuda a verlos, casi a tocarlos, ¿no?
Vale, para empezar, a ver, imaginemos la diferencia de una forma sencilla. Pensemos en dos coches, van por una carretera súper recta.
Uno, eh, lleva como el control de crucero puesto, velocidad fija, ni más ni menos. Eso sería, digamos, el MRU.
El otro coche, en cambio, pues o está pisando el acelerador pero siempre igual, de forma constante, o está frenando, también de forma constante.
Su velocidad sí que cambia, pero el ritmo al que cambia, ese es siempre el mismo. Ese es el MRUA.
Entonces, ¿cuál dirías que es el punto clave que los separa?
Pues mira, la aceleración. Es así de simple y, a la vez, es fundamental. En el MRU, la aceleración es cero, cero patatero. No hay cambios en la velocidad.
En el MRUA, en cambio, sí hay aceleración, y esta es constante y, ojo, distinta de cero.
Esa presencia o ausencia de aceleración constante es lo que define todo: cómo se mueve, cómo lo describimos con fórmulas y, como veremos, cómo son sus gráficas.
Perfecto. Empecemos entonces por el más, eh, sencillo quizás, el MRU. Movimiento en línea recta y, como decías, a velocidad constante.
Esto quiere decir que si algo va a, no sé, 10 m/s, pues recorre 10 metros el primer segundo, otros 10 el segundo, otros 10 el tercero, siempre igual.
Y la aceleración, por lo tanto, es cero, ¿verdad? 0 m/s².
Quienes estéis ahora mismo con el simulador delante, esto lo podéis ver muy fácil. Si vais al deslizador de la aceleración ($a$) y lo ponéis en 0.0 m/s², y luego le dais una velocidad inicial ($v_0$) que no sea cero, claro, pongamos 15 m/s, por ejemplo.
Le dais a iniciar, ¿y qué se ve? Pues el coche se mueve, eh, sin cambiar su rapidez, va suave. Fijaos en la flechita de la velocidad, la que está sobre el coche. Su tamaño no cambia y apunta siempre igual.
Y si abrís la tabla de datos, veréis que el valor en la columna $v$ (m/s) se queda fijo en 15, todo el rato.
Exacto. Y aquí es donde las gráficas, bueno, nos cuentan la historia visualmente. Para el MRU son muy, muy claras. Hay tres importantes.
La primera, la de posición frente al tiempo ($x-t$). Lo que se ve es una línea recta inclinada. Esa inclinación, lo que llamamos la pendiente, representa precisamente esa velocidad constante. Si va más rápido, la recta está más inclinada. Si fuera hacia la izquierda, pues inclinada hacia abajo, pero siempre una recta.
Luego está la de velocidad frente al tiempo ($v-t$). Esta es súper simple: una línea recta horizontal, completamente plana.
¿Por qué? Pues porque la velocidad no cambia. Estará a la altura del valor que hayamos puesto, a 15 m/s en tu ejemplo.
Y la tercera, la de aceleración frente al tiempo ($a-t$). También es una línea recta horizontal, pero esta vez está justo sobre el eje del tiempo, o sea, en el valor cero. Confirma que la aceleración es nula, no hay más.
Y para saber dónde estará el objeto en cualquier momento, hay una fórmula muy directa para el MRU. Atención a cómo se lee:
$$
x(t) = x_0 + v \cdot t
$$
Vamos a ver qué es cada cosa. $x(t)$ es la posición final en un instante $t$.
Es igual a $x_0$, que es la posición inicial de donde salió, más $v \cdot t$, que es la velocidad constante $v$ multiplicada por el tiempo $t$ que ha estado moviéndose.
Eso es. Y lo bueno es ver cómo esto encaja perfectamente con el simulador. Imagina que ponemos $x_0=10$ m, $v_0=20$ m/s y $a=0$, claro.
Antes de darle a iniciar, podemos usar la fórmula para predecir. A ver, ¿dónde estará a los 4 segundos? Calculamos: $x(4)=10+20 \cdot 4$. Es decir, $10+80$, pues 90 metros. Nuestra predicción es 90 metros.
Y ahora, viene la magia. Le damos a iniciar en el simulador, dejamos que pasen esos 4 segundos, miramos la gráfica de posición $x-t$ justo en $t=4$ s, o buscamos en la tabla de datos la fila de $t=4$ s y ver el valor de $x$.
Aparece... pues debería ser 90 metros, exactamente 90.
Genial. Es justo esa conexión, ¿no? entre la fórmula y lo que vemos. Confirma que la teoría funciona. Vale, pues el MRU parece bastante claro.
Pasemos ahora al otro, al MRUA: Movimiento Rectilíneo Uniformemente Acelerado. Aquí la clave es que la velocidad sí cambia, pero lo hace de manera uniforme, a un ritmo constante.
La aceleración puede ser positiva, que en sentido positivo, pues hace que vaya más rápido, o puede ser negativa. Y aquí, bueno, ya adelantamos que negativa no siempre significa frenar, eh, lo veremos.
En el simulador, para ver un MRUA, ¿qué hacemos?
Pues muy fácil, cualquier valor que le pongas al deslizador de aceleración, $a$, que no sea 0.0 m/s², ya te da un MRUA. Pongamos un ejemplo: una velocidad inicial $v_0$ de 5.0 m/s y una aceleración $a$, no sé, de 1.0 m/s².
Vale. Le damos a iniciar, ¿qué deberíamos observar?
Pues que el coche va cada vez más deprisa. La flecha de velocidad, el vector, se irá haciendo más y más grande. Y además, aparecerá otra flecha, la de la aceleración, que esa sí se mantiene constante en tamaño y dirección.
Ah, claro. ¿Y en la tabla de datos?
Pues si miras la columna $v$ (m/s), deberías ver cómo aumenta en 1.0 cada segundo que pasa. Si empezó en 5, al segundo será 6, luego 7, 8... va sumando uno cada segundo. Eso es una aceleración de 1 m/s².
Y las gráficas del MRUA, claro, son diferentes a las del MRU. Tienen otra pinta. La gráfica posición versus tiempo ($x-t$) ya no es una recta, ahora es una parábola, una curva.
La forma de esa curva nos dice cosas. Si se abre hacia arriba como una U, significa que la aceleración es positiva. Si se abre hacia abajo, como una U invertida, la aceleración es negativa.
Luego, la gráfica velocidad versus tiempo ($v-t$), esta vuelve a ser una línea recta, como en el MRU, pero ahora está inclinada, ya no es horizontal.
Y aquí viene algo importante: la pendiente, la inclinación de esta recta, es exactamente el valor de la aceleración constante $a$. Si la recta sube, $a$ es positiva; si baja, $a$ es negativa.
Y finalmente, la gráfica aceleración versus tiempo ($a-t$) sigue siendo una línea recta horizontal, porque la aceleración es constante. Pero ahora ya no está en el cero, estará a la altura del valor de $a$ que hayamos elegido.
Si pusimos $a=1.0$ m/s², pues la línea estará en 1.0.
Vale, entendido. Y para describir esto con matemáticas, necesitamos, creo que eran dos ecuaciones principales, ¿no?
Eso es, dos fórmulas fundamentales para el MRUA.
A ver, la primera es para la velocidad en cualquier instante. Se lee:
$$
v(t) = v_0 + a \cdot t
$$
O sea, la velocidad final, $v(t)$, es la velocidad inicial, $v_0$, más lo que ha cambiado por la aceleración, que es la aceleración $a$ por el tiempo $t$.
Así es. Perfecto.
Y la segunda es para la posición. Esta es un poquito más larga:
$$
x(t) = x_0 + v_0 t + \frac{1}{2} a t^2
$$
Aquí tenemos: posición final, $x(t)$, igual a la inicial, $x_0$, más lo que se movería con la velocidad inicial si no hubiera aceleración, $v_0 t$, más —y aquí está el término nuevo— $\frac{1}{2}at^2$.
Ojo, ese $t$ al cuadrado.
Exacto, $\frac{1}{2}at^2$. Ese término cuadrático es el que refleja el efecto acumulado de la aceleración sobre la posición y es el responsable de que la gráfica $x-t$ sea una parábola.
Son las dos herramientas clave para predecir dónde estará y qué velocidad tendrá un objeto en MRUA, ¿no?
Justo. Si conoces cómo empieza ($x_0, v_0$) y cuál es su aceleración constante ($a$), puedes saberlo todo sobre su futuro movimiento rectilíneo.
Y ahora llegamos a un punto que a veces lía un poco. Hemos hablado de aceleración positiva y negativa. Una pregunta muy típica es: ¿si la aceleración es negativa, significa sí o sí que el objeto está frenando?
Ah, muy buena pregunta. Porque la respuesta corta es: no, no necesariamente. Es una confusión súper habitual. A ver, una aceleración negativa lo que indica es que el vector aceleración apunta en la dirección que hemos decidido llamar negativa.
Normalmente en las simulaciones es hacia la izquierda. Pero que frene o no, eso depende de cómo sea esa aceleración comparada con la velocidad que ya tiene el objeto.
Podemos, podemos probarlo en el simulador para verlo claro.
Claro que sí. Es la mejor manera. Probad, quienes tengáis el simulador, estos dos casos. Caso 1: Frenada. Poned una velocidad inicial positiva, bastante alta, por ejemplo, $v_0 = 20.0$ m/s. Se mueve a la derecha.
Y ahora, una aceleración negativa, por ejemplo, $a = -1.0$ m/s². Le dais a iniciar. ¿Qué se ve? Claramente, el coche va frenando. La velocidad disminuye, el vector velocidad se acorta. Si lo dejáis tiempo, incluso se parará, y puede que empiece a moverse hacia atrás, hacia la izquierda.
Aquí, la velocidad (positiva) y la aceleración (negativa) tienen signos opuestos. Resultado: frena.
Vale, ese es el caso que uno esperaría, quizás. ¿Y el otro?
Caso 2: Aceleración negativa que no frena. Ahora haced algo distinto. Poned una velocidad inicial que ya sea negativa, por ejemplo, $v_0=-10.0$ m/s. Ya se está moviendo hacia la izquierda.
Y mantened una aceleración también negativa, por ejemplo, $a=-1.0$ m/s².
Mmm, ¿qué pasará ahora? ¿Velocidad negativa, aceleración negativa?
Pues sorpresa: le das a iniciar y el coche no frena, al contrario, acelera hacia la izquierda. Se mueve cada vez más rápido, pero en dirección negativa. El vector velocidad, que ya apuntaba a la izquierda, se hace más largo.
En este caso, la velocidad y la aceleración tienen el mismo signo, ambas negativas. Resultado: la rapidez aumenta.
¡Ostras! Entendido. Entonces, la clave no es solo el signo de la aceleración, sino compararlo con el signo de la velocidad.
Si los signos son opuestos (uno positivo, otro negativo), el objeto frena, su rapidez disminuye. Y si los signos son iguales (ambos positivos o ambos negativos), el objeto acelera, su rapidez aumenta en la dirección que sea.
Exactamente. Esa es la idea. Aceleración negativa no es sinónimo de frenar, es una cuestión de dirección relativa entre velocidad y aceleración.
Muy, muy claro ahora. Y esto, supongo, también se ve en las pendientes de las gráficas que mencionaste antes.
Efectivamente. En el MRUA, la gráfica $v-t$ es una recta inclinada. Si la aceleración $a$ es negativa, la pendiente de esa recta será negativa, o sea, la recta irá hacia abajo. Pero si la velocidad inicial también era negativa, como en el segundo caso que probamos, aunque la recta vaya hacia abajo en la gráfica, estará representando velocidades cada vez más negativas, o sea, mayor rapidez hacia la izquierda. Hay que interpretar bien la gráfica.
Genial. Bueno, ya sabemos diferenciar MRU y MRUA, interpretar sus gráficas, y hemos aclarado el mito de la aceleración negativa. Pero, eh, ¿cómo podemos estar realmente seguros de que esas fórmulas matemáticas que dimos, la de $v(t)$ y la de $x(t)$, describen de verdad lo que vemos moverse en la pantalla del simulador?
Pues... comprobándolo, haciendo una verificación directa. Es un proceso muy útil porque conecta la teoría (las ecuaciones) con la observación experimental, aunque aquí sea virtual. Podemos seguir unos pasos sencillos.
Paso 1: Elegimos unas condiciones iniciales para un MRUA en el simulador. Vamos a poner otras distintas. Por ejemplo, empezamos en el origen, $x_0 = 0$. Le damos una velocidad inicial hacia la izquierda: $v_0 = -15$ m/s, y una aceleración positiva: $a = 2$ m/s².
Vale.
$x_0=0$, $v_0=-15$, $a=2$. Paso 2: Antes de darle a iniciar, usamos una de las fórmulas para predecir algo. Por ejemplo, ¿qué velocidad tendrá a los 5 segundos? Usamos $v(t) = v_0 + a t$.
Calculamos: $v(5) = -15 + 2 \cdot 5$. Eso es $-15+10$, que da $-5$ m/s. Nuestra predicción es que a los 5 segundos, la velocidad será $-5$ m/s.
Fíjate que empezó en -15 m/s. Como la aceleración es positiva (hacia la derecha), está consiguiendo que frene su movimiento hacia la izquierda.
Entendido. La predicción es $-5$ m/s a los 5 segundos.
Paso 3: Ahora sí, ejecutamos la simulación. Dale a iniciar. Paso 4: Dejamos que corra hasta $t=5$ s y observamos qué dice el simulador en ese instante.
Podemos mirar la gráfica $v-t$, a ver qué valor tiene en $t=5$ s, o ir a la tabla de datos y buscar la fila $t=5$ s y ver el valor de $v$.
Vale, mirando la tabla o la gráfica en $t=5$.
Paso 5: ¿Coincide el valor que muestra el simulador con nuestra predicción de $-5$ m/s?
Si hemos hecho bien los cálculos y la simulación funciona como debe, debería coincidir.
Exacto. Y si coincide, acabamos de verificar experimentalmente, bueno, virtualmente, que la ecuación cinemática describe correctamente el movimiento simulado. Podríamos hacer lo mismo con la ecuación de posición para predecir dónde estará y comprobarlo también.
Es una forma fantástica de ver que las fórmulas no son solo letras y números, sino que realmente describen cómo se mueven las cosas. O al menos, cómo se mueven en esta simulación, que, bueno, está programada para seguir esas leyes físicas.
Bueno, pues creo que hemos cubierto bastante terreno hoy, ¿eh? Hemos visto las diferencias entre MRU y MRUA, sobre todo por la aceleración. Hemos aprendido a identificarlos en el simulador, a leer sus gráficas características (esas rectas y parábolas).
Hemos aclarado esa duda común sobre la aceleración negativa. Y finalmente, hemos visto cómo las ecuaciones y la simulación se validan la una a la otra.
Sí, ha sido una buena exploración de estos conceptos básicos pero fundamentales de la cinemática. Y quizás para terminar, podríamos dejar una idea en el aire, algo para darle una vuelta. Hemos visto cómo usamos las ecuaciones para ir, digamos, del presente (las condiciones iniciales) al futuro (predecir posición y velocidad).
Pero, ¿y si quisiéramos hacer el camino inverso?
¿El camino inverso? ¿A qué te refieres exactamente?
Pues, piensa en un pequeño desafío de diseño. Imagina que queremos que nuestro cochecito virtual termine exactamente en una posición, digamos, $x=50$ m. Y no solo eso, sino que queremos que llegue ahí con velocidad final $v=0$ m/s, o sea, que se pare justo en los 50 metros.
Y queremos que lo haga después de, no sé, $t=10$ segundos. Si sabemos que empezamos desde $x_0=0$, ¿podríamos usar las ecuaciones del MRUA para calcular hacia atrás? Es decir, para averiguar qué velocidad inicial $v_0$ tendríamos que darle y qué aceleración constante $a$ necesitaríamos aplicar para conseguir exactamente ese resultado final tan específico.
Oye, qué interesante. Sería como... como usar la física no solo para predecir lo que va a pasar, sino para diseñar, para programar un movimiento concreto que queremos que ocurra. Calcular las condiciones iniciales o la aceleración necesaria a partir del resultado final deseado.
Justo eso. Es darle una vuelta de tuerca que muestra lo potentes que son estas herramientas, las ecuaciones y la simulación juntas. ¿Os animáis a intentarlo, a calcular esa $v_0$ y esa $a$, y luego comprobarlo en el simulador?
Ahí queda el reto lanzado. Sin duda, una pregunta genial para seguir jugando y experimentando. Animamos a todos en Aula Quest a que sigáis trasteando con el simulador, probad valores diferentes, mirad cómo cambian las gráficas, conectad todo con las ideas que hemos visto hoy. La mejor forma de aprender es explorando por uno mismo. Hasta la próxima exploración.
Teoría y Práctica del Movimiento Rectilíneo Uniforme (MRU)
¿Qué es el Movimiento Rectilíneo Uniforme (MRU)?
El MRU describe el movimiento de un cuerpo que se desplaza en línea recta a una velocidad constante y, por lo tanto, con aceleración nula. Esto significa que recorre distancias iguales en tiempos iguales.
Ejemplo práctico: Imagina un coche en una autopista recta y sin tráfico que mantiene el velocímetro clavado en 100 km/h. Ese coche está describiendo un MRU.
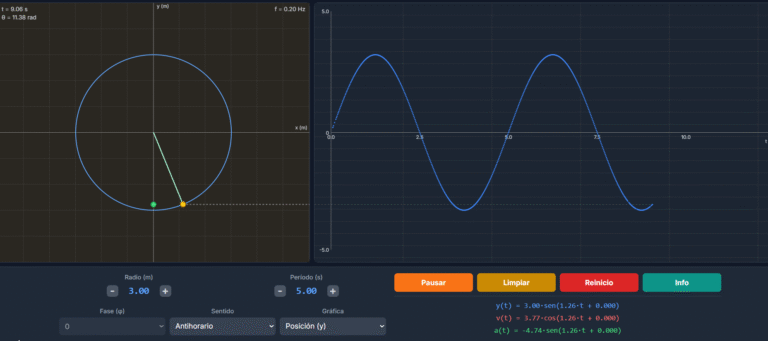
¿Cómo interpreto las gráficas de cinemática (x-t, v-t, a-t) en un MRU?
Las gráficas son la representación visual del movimiento. Para un MRU, son muy características:
- Gráfica Posición vs. Tiempo (x-t): Es una línea recta inclinada. La pendiente representa la velocidad.
- Gráfica Velocidad vs. Tiempo (v-t): Es una línea recta horizontal, ya que la velocidad no cambia.
- Gráfica Aceleración vs. Tiempo (a-t): Es una línea recta sobre el eje x (valor cero), porque la aceleración es nula.
x(t) = x₀ + v · t
¿Qué significa el área bajo la gráfica v-t en un MRU?
Un concepto muy importante en cinemática es que el área bajo la curva de la gráfica velocidad-tiempo (v-t) representa la distancia recorrida.
En un MRU, la gráfica v-t es una línea horizontal. El área bajo ella, hasta un tiempo 't', forma un rectángulo. La base del rectángulo es el tiempo (t) y la altura es la velocidad (v). Por lo tanto, el área es base × altura = v · t, que es exactamente la fórmula de la distancia recorrida en un MRU (asumiendo x₀=0).
Teoría y Práctica del Movimiento Rectilíneo Uniformemente Acelerado (MRUA)
¿Cuál es la diferencia clave del MRUA?
En el MRUA, la velocidad cambia de manera uniforme porque existe una aceleración constante y distinta de cero. Si la aceleración tiene el mismo sentido que la velocidad, el cuerpo acelera. Si tiene sentido contrario, el cuerpo frena.
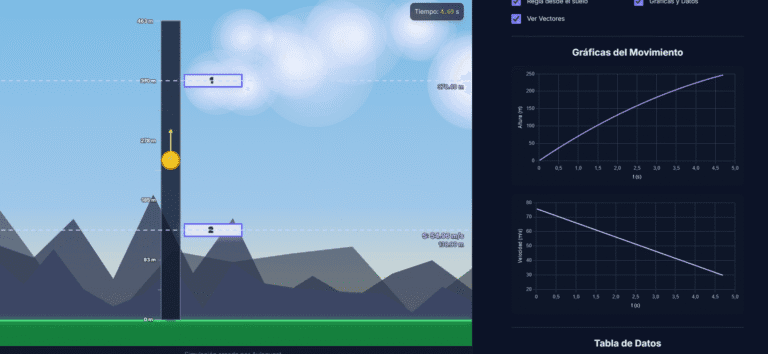
¿Cómo son las gráficas de un MRUA (acelerando)?
Cuando un objeto acelera (su velocidad y aceleración tienen el mismo signo):
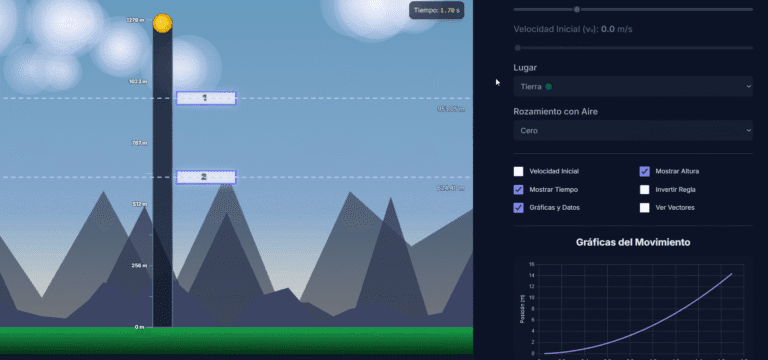
- Gráfica Posición vs. Tiempo (x-t): Es una parábola que se abre hacia arriba (si a > 0) o hacia abajo (si a < 0 y v < 0).
- Gráfica Velocidad vs. Tiempo (v-t): Es una línea recta inclinada. La pendiente es la aceleración.
- Gráfica Aceleración vs. Tiempo (a-t): Es una línea recta horizontal en el valor de la aceleración.
v(t) = v₀ + a · t
x(t) = x₀ + v₀ · t + ½ a · t²
¿Y cómo son las gráficas en una frenada?
Una frenada ocurre cuando la velocidad y la aceleración tienen signos opuestos (ej: v > 0 y a < 0). Observa las diferencias:
- Gráfica Posición vs. Tiempo (x-t): Sigue siendo una parábola, pero ahora se "aplana" hasta alcanzar un máximo (cuando v=0) y luego puede empezar a bajar. Se abre hacia abajo si la aceleración es negativa.
- Gráfica Velocidad vs. Tiempo (v-t): Es una recta inclinada que desciende, cruza el eje x (v=0) y continúa en valores negativos, indicando que el objeto ha empezado a moverse en sentido contrario.
- Gráfica Aceleración vs. Tiempo (a-t): Es una línea recta horizontal, pero en el lado negativo del eje.
¿Cómo se relacionan las fórmulas con un simulador?
¡Es una conexión directa! Cuando usas un simulador, los valores que ajustas son las "condiciones iniciales" de las fórmulas:
- Posición Inicial (x₀): Es el punto de partida del objeto. En la fórmula, es el término `x₀`.
- Velocidad Inicial (v₀): Es la velocidad que tiene el objeto justo cuando pulsas "Iniciar". Corresponde al término `v₀`.
- Aceleración (a): Es el cambio constante de velocidad que aplicas. Es el término `a` en las ecuaciones.
Al pulsar "Iniciar", el simulador simplemente calcula `x(t)` y `v(t)` para cada instante de tiempo `t` usando las fórmulas del MRUA. Los botones "Ver Tabla" o "Ver Gráficas" te muestran esos resultados de forma numérica o visual.
Historias fascinantes en el blog de Aulaquest
Quiz de Cinemática: MRU y MRUA
Pon a prueba tu dominio del movimiento rectilíneo, las gráficas y las ecuaciones de la cinemática.
Elige un modo de juego:
Pregunta 1 de 10
Puntuación: 0
¡Desafío completado!
Tu puntuación final:
0
Análisis de Rendimiento
Zona de Actividades de tu Profesor
Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.
¿Tu última clase con la simulación fue un éxito?
Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Crear una actividad es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.
- 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
- 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
- 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
📤 Subir mi actividad
*Esto es solo para profes. Si lo eres, pide tu acceso.
Simulaciones en fisica
¿CUÁL SERÁ TU PRÓXIMO DESCUBRIMIENTO?
¡Gran trabajo con esta simulación! Ahora puedes ampliar tus horizontes en otras áreas del conocimiento. ¿Por dónde quieres seguir?
