Simulador de Plano Inclinado Online

¡Bienvenido a tu laboratorio de dinámica online! Un plano inclinado es una de las "máquinas simples" fundamentales en física. Es simplemente una superficie plana con un ángulo respecto a la horizontal. Su utilidad es inmensa: nos permite levantar objetos pesados aplicando menos fuerza.

Este simulador de física de plano inclinado te permitirá:

• Visualizar y entender el diagrama de fuerzas en un plano inclinado.
• Analizar cómo el ángulo, la masa y el rozamiento afectan al movimiento.
• Aplicar la Segunda Ley de Newton para calcular la aceleración.
• Estudiar la conservación de la energía y el trabajo realizado por las fuerzas.

Para analizar el movimiento, lo primero es dibujar un diagrama de cuerpo libre. En el simulador, las fuerzas se dibujan por ti. Las más importantes son:

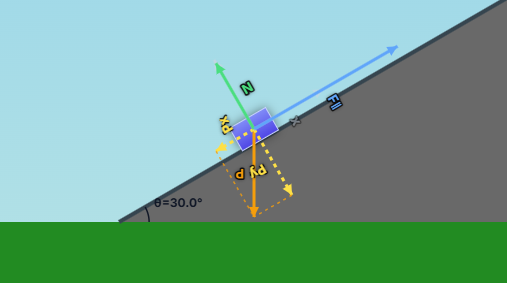
• Peso $P$: Es la fuerza de la gravedad, siempre apunta verticalmente hacia abajo. Se calcula como $P = m \cdot g$.
• Fuerza Normal $N$: Es la fuerza de soporte que ejerce el plano sobre el bloque. Es siempre perpendicular a la superficie.
• Fuerza de Rozamiento $F_r$: Se opone al movimiento o al intento de movimiento, y es siempre paralela a la superficie.

El truco en un plano inclinado es descomponer el peso $P$ en dos componentes, ya que no es ni paralelo ni perpendicular al plano:

La fuerza de rozamiento es una fuerza que se opone al movimiento entre superficies en contacto. En el simulador, puedes activarla y ver su efecto. Hay dos tipos:

• Rozamiento Estático $F_{r,e}$: Actúa cuando el cuerpo está en reposo. Impide que el movimiento comience. Su valor es variable: es igual y opuesto a la fuerza que intenta mover el objeto, hasta un valor máximo. $F_{r,e, \text{max}} = \mu_e \cdot N$. Si la fuerza motriz (como $P_x$) supera este valor, ¡el objeto empieza a moverse!
• Rozamiento Cinético $F_r$: Actúa cuando el cuerpo ya está en movimiento. Generalmente, es un poco menor que el estático y su valor es constante. Se calcula con la fórmula:

Donde $\mu_e$ y $\mu_c$ son los coeficientes de rozamiento estático y cinético, respectivamente.

La Segunda Ley de Newton, $\Sigma F = m \cdot a$, es la clave para calcular la aceleración. La aplicamos por separado en los ejes paralelo (X) y perpendicular (Y) al plano:

El bloque no salta ni se hunde, así que no hay movimiento en este eje. Las fuerzas están equilibradas.

Esto es muy importante: nos permite calcular la Fuerza Normal, que a su vez necesitamos para la fuerza de rozamiento.

Aquí es donde ocurre el movimiento. Sumamos las fuerzas que van a favor del movimiento (motrices) y restamos las que van en contra (resistentes).

Por ejemplo, para un bloque que desliza hacia abajo con rozamiento, la fórmula sería:

Dependiendo de las fuerzas aplicadas, podemos analizar varios escenarios. En todos ellos, la clave es identificar qué fuerzas ayudan al movimiento (motrices) y cuáles se oponen (resistentes) para aplicar correctamente la Segunda Ley de Newton. Usaremos $\mu_c$ como el coeficiente de rozamiento cinético.

Es un buen punto de partida. Al no haber inclinación, el peso no tiene componente paralela ($P_x=0$) y la fuerza normal $N$ es igual al peso ($N=mg$).

• Fuerzas Motrices: Una fuerza externa aplicada $F$.
• Fuerzas Resistentes: La fuerza de rozamiento $F_r$.

Es el caso más simple: soltamos el bloque y la gravedad hace su trabajo. No hay fuerzas externas aplicadas.

• Fuerzas Motrices: La componente X del peso $P_x$.
• Fuerzas Resistentes: La fuerza de rozamiento $F_r$.

Además de la gravedad, una fuerza externa $F_{\parallel}$ empuja el bloque hacia abajo, en la misma dirección del plano.

• Fuerzas Motrices: El peso $P_x$ y la fuerza externa $F_{\parallel}$.
• Fuerzas Resistentes: La fuerza de rozamiento $F_r$.

El cuerpo se lanza hacia arriba y ninguna fuerza sigue empujándolo. La gravedad y el rozamiento lo frenarán.

• Fuerzas Motrices: Ninguna.
• Fuerzas Resistentes: El peso $P_x$ y el rozamiento $F_r$. Ambas apuntan hacia abajo.

La aceleración será negativa, indicando que el cuerpo está frenando.

Una fuerza externa $F_{\parallel}$ empuja constantemente el bloque hacia arriba, paralela al plano.

• Fuerzas Motrices: La fuerza externa $F_{\parallel}$.
• Fuerzas Resistentes: El peso $P_x$ y el rozamiento $F_r$.

Una fuerza horizontal $F_H$ empuja el bloque. Esta fuerza tiene un doble efecto: una parte empuja el bloque hacia arriba del plano y otra lo "aprieta" más contra la superficie, aumentando el rozamiento.

Primero, descomponemos la fuerza horizontal $F_H$:

• Su componente paralela, $F_{H,x} = F_H \cos(\theta)$, es la que empuja el bloque hacia arriba.
• Su componente perpendicular, $F_{H,y} = F_H \sin(\theta)$, presiona el bloque contra el plano.

Esta presión extra aumenta la fuerza normal. Ahora, la normal $N$ debe equilibrar tanto $P_y$ como $F_{H,y}$:

Con esto, podemos definir las fuerzas motrices y resistentes:

• Fuerzas Motrices: La componente paralela de la fuerza horizontal, $F_{H,x}$.
• Fuerzas Resistentes: La componente paralela del peso $P_x$ y la nueva fuerza de rozamiento $F_r = \mu_c N$.

Las gráficas son una herramienta visual muy potente. Activa "Ver Gráficas" en el simulador para verlas en tiempo real.

Si dejas caer un bloque sin rozamiento, la única fuerza motriz es $P_x$. Como es constante, la aceleración es constante.

• Gráfica Aceleración vs. Tiempo: Será una línea horizontal. La aceleración no cambia.
• Gráfica Velocidad vs. Tiempo: Será una línea recta con pendiente negativa. La velocidad se vuelve más negativa (aumenta en magnitud) de manera uniforme.
• Gráfica Altura vs. Tiempo: Será una parábola descendente.

La energía también nos da mucha información.

• Sin Rozamiento (Gráfica Izquierda): La Energía Mecánica Total $E_m$ se conserva. Es una línea horizontal. Verás cómo la Energía Potencial $E_p$ se transforma en Energía Cinética $E_c$ a medida que el bloque cae.
• Con Rozamiento (Gráfica Derecha): La Energía Mecánica Total disminuye. Esta energía "perdida" no desaparece, sino que se transforma en calor por el trabajo que realiza la fuerza de rozamiento.