Simulador de Colisiones 1D
🧪 Laboratorio de Colisiones unidimensionales
Este laboratorio virtual te invita a explorar colisiones en una dimensión con distintos escenarios: desde choques perfectamente elásticos hasta encuentros donde los objetos se quedan unidos como si fueran velcro.
Para dominar conceptos clave como choque elástico, colisión inelástica y transferencia de movimiento
- 🔗 Dinámica | Energía y Trabajo ↗️
- 🎓 Nivel educativo: Bachillerato
- ⚙️ Dificultad: Facil (3/10)
- 📈 Visitas: 418
📎 Código para incrustar
¿Eres profe, divulgador o webmaster?
Puedes incrustar esta simulación en tu web o blog sin problema.
Solo pedimos dos cosas básicas:
- ✅ Que cites la fuente: AulaQuest.com
- 🚫 Que no la uses con fines comerciales
Este es el código que puedes copiar:
<iframe
src="https://aulaquest.github.io/colision-de-bloques-1d/"
width="100%"
height="560"
style="border: 1px solid #ccc; border-radius: 8px;"
allowfullscreen
title="Simulación de Colisiones 1D AulaQuest"></iframe>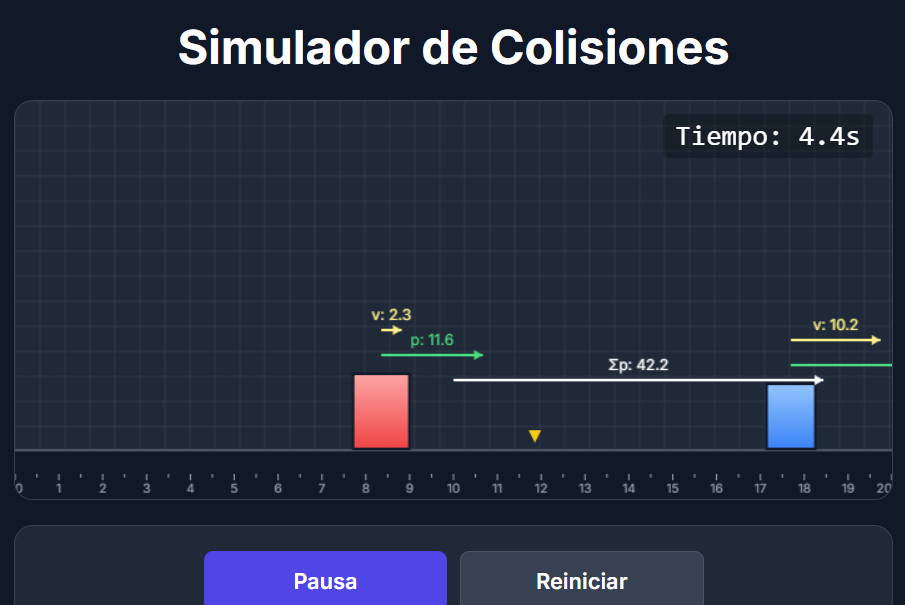
AulaQuest
Iniciando simulación...
Colisiones Unidimensionales: Momento, Energía y Centro de Masas
💥 ¡Al Choque! Entendiendo las Colisiones de Bloques
Imagina dos bloques, uno rojo y otro azul, deslizándose por una pista sin rozamiento. ¿Qué pasa cuando se encuentran? ¡Chocan!
Pero en física, un "choque" o colisión es mucho más que un simple golpe. Es una interacción intensa y breve donde los objetos intercambian momento y energía. ¿El resultado? Depende de las reglas del juego: su masa, su velocidad y el tipo de colisión.
🏃♂️ Momento Lineal: La "Inercia en Movimiento"
Antes de hablar de choques, necesitamos conocer a nuestro protagonista: el momento lineal (o cantidad de movimiento). Piensa en él como una medida de "cuánta movida" lleva un objeto. No es lo mismo parar a una persona que camina lento que a un camión a toda velocidad. El momento combina la masa y la velocidad en una sola idea. Se representa con la letra \( p \).
Un objeto con más masa o más velocidad tiene más momento lineal. Su cálculo es muy sencillo:
Donde:
- \( p \) es el momento lineal (se mide en kg·m/s).
- \( m \) es la masa del objeto (en kg).
- \( v \) es la velocidad del objeto (en m/s).
Importante: La velocidad tiene dirección. En un sistema unidimensional como el de nuestra simulación, la velocidad puede ser positiva (hacia la derecha) o negativa (hacia la izquierda). ¡El signo del momento lineal también depende de ello!
🤝 La Regla de Oro: La Conservación del Momento
Aquí viene la ley más importante de las colisiones, la que se cumple SIEMPRE (en sistemas aislados, como nuestra pista sin rozamiento). La ley de conservación del momento lineal dice que el momento total de un sistema antes de la colisión es exactamente igual al momento total después de la colisión.
El momento puede transferirse de un bloque a otro, pero la suma total no cambia. Es como si los bloques se "pasaran" el movimiento, pero nada se pierde por el camino.
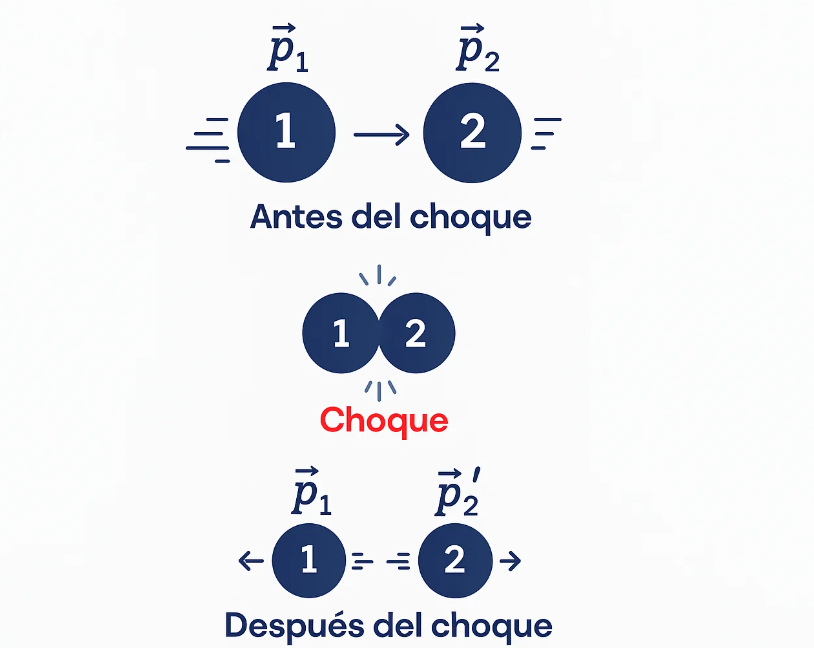
Matemáticamente, lo expresamos así:
¡Pruébalo en el simulador! Observa el valor del "momento total". Verás que, sin importar qué tipo de choque configures, este valor permanece constante antes, durante y después de la colisión.
¡Ojo, que tiene truco! La conservación del momento solo se cumple si el sistema está aislado, es decir, si nadie mete la mano ni actúan fuerzas externas. En nuestra simulación, eso significa: mientras los bloques chocan entre ellos sin tocar las paredes, el momento total se conserva. Pero en cuanto uno rebota contra una pared (aunque sea invisible y transparente), ya hay una fuerza externa actuando.
¿Resultado? Su momento cambia de signo (porque cambia de dirección), y el sistema deja de ser cerrado. A partir de ese instante, el momento total ya no se conserva.
📍 El Centro de Masas: El Punto que no se Inmuta
El Centro de Masas (CM) es el "punto de equilibrio" de nuestro sistema de dos bloques. Es un punto imaginario que se mueve como si toda la masa del sistema estuviera concentrada ahí. Su posición se calcula haciendo una media ponderada de las posiciones de los bloques:
Lo realmente interesante es su velocidad. Gracias a la conservación del momento, la velocidad del Centro de Masas se mantiene constante durante toda la colisión. Los bloques pueden chocar, rebotar o quedarse pegados, pero el CM seguirá su camino tranquilamente, a la misma velocidad, como si nada hubiera pasado.
Esta fórmula muestra que la velocidad del CM depende de la cantidad de movimiento total del sistema dividido entre la masa total. Si no hay fuerzas externas, esa cantidad de movimiento se conserva… y el CM sigue avanzando sin alterarse.
En el simulador, observa cómo se desplaza este punto. Su trayectoria es predecible, constante y suave, completamente ajena al caos del choque entre los bloques.
⚡ Energía Cinética: La Energía del Movimiento
Además del momento, los objetos en movimiento tienen energía cinética (\( E_c \)), que es la energía asociada a su velocidad. A diferencia del momento, la energía cinética no es un vector, es un escalar (un número sin dirección) y siempre es positiva.
La energía cinética total del sistema es simplemente la suma de las energías cinéticas de cada bloque. Y aquí viene la gran pregunta: ¿se conserva también la energía cinética en una colisión? La respuesta... depende del tipo de choque.
🤯 Los 3 Tipos de Colisiones
La conservación o no de la energía cinética es lo que nos permite clasificar las colisiones en tres tipos. ¡Vamos a verlos!
1. Choque Perfectamente Elástico
Es el choque "ideal", el más ordenado. En una colisión perfectamente elástica, tanto el momento lineal como la energía cinética total se conservan. Es como el choque de dos bolas de billar perfectas. No se pierde nada de energía en forma de calor, sonido o deformación.
- ✅ Momento lineal: Se conserva.
- ✅ Energía cinética: Se conserva.
- Los bloques rebotan el uno contra el otro.
En el simulador, puedes explorar casos curiosos. Por ejemplo, si dos bloques de igual masa chocan elásticamente y uno de ellos está quieto, ¡intercambian sus velocidades! Pruébalo.
2. Choque Perfectamente Inelástico
Este es el extremo opuesto. En una colisión perfectamente inelástica, los bloques chocan y se quedan pegados, moviéndose juntos como un solo objeto después del impacto.
Aquí, el momento lineal sigue conservándose (¡siempre lo hace!), pero la energía cinética no se conserva. De hecho, es el tipo de choque donde se pierde la máxima cantidad de energía cinética posible, que se disipa en forma de calor, sonido y, sobre todo, en la deformación que los une.
- ✅ Momento lineal: Se conserva.
- ❌ Energía cinética: No se conserva (pérdida máxima).
- Los bloques se quedan unidos tras el choque (\( v_{1, \text{después}} = v_{2, \text{después}} \)).
Fíjate en el simulador cómo, al quedarse pegados, la energía cinética total del sistema disminuye drásticamente justo después del impacto.
3. Choque Inelástico (el del mundo real)
La mayoría de las colisiones en el mundo real (un choque de coches, una pelota que bota y no sube a la misma altura inicial) son inelásticas. Se sitúan en un punto intermedio entre los dos casos anteriores.
- ✅ Momento lineal: Se conserva.
- ❌ Energía cinética: No se conserva, pero se pierde menos que en el choque perfectamente inelástico.
- Los bloques rebotan, pero no con la misma "energía" que en un choque elástico.
En resumen: la única ley que debes tatuarte a fuego es la conservación del momento lineal. La energía cinética, en cambio, es la que nos cuenta la "historia" de la colisión: si fue un rebote perfecto o un abrazo pegajoso.
¡Ahora te toca a ti! Juega con todas las variables en la simulación. Configura choques elásticos, inelásticos y perfectamente inelásticos. Comprueba cómo el momento total nunca cambia y observa qué pasa con la energía. ¡La mejor forma de aprender es experimentar!
Quiz de Colisiones 1D
Pon a prueba tu conocimiento sobre momento lineal, energía cinética y los distintos tipos de choques.
Pregunta 1 de 10
Puntuación: 0
¡Desafío completado!
Tu puntuación final:
Zona de Actividades de tu Profesor
Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.
¿Tu última clase con la simulación fue un éxito?
Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Subirla a la Zona Profe es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.
- 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
- 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
- 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
No necesitas dar la clase perfecta
Solo necesitas que tus alumnos entiendan. Usa nuestras simulaciones y cambia el chip sin perder tiempo ni energía.
Zona Profe¿Sugerencias o errores?
Si encuentras algún fallo en las simulaciones o tienes ideas para mejorarlas, nos encantaría escucharte.
ContactarSimulaciones en Física
No necesitas dar la clase perfecta
Solo necesitas que tus alumnos entiendan. Usa nuestras simulaciones y cambia el chip sin perder tiempo ni energía.
Zona Profe¿Sugerencias o errores?
Si encuentras algún fallo en las simulaciones o tienes ideas para mejorarlas, nos encantaría escucharte.
Contactar¿CUÁL SERÁ TU PRÓXIMO DESCUBRIMIENTO?
¡Gran trabajo con esta simulación! Ahora puedes ampliar tus horizontes en otras áreas del conocimiento. ¿Por dónde quieres seguir?