La Guerra de un Hombre contra los Círculos Perfectos: La Épica Historia de las Leyes de Kepler
Descubre cómo la obsesión de dos genios rivales, Tycho Brahe y Johannes Kepler, rompió con 2.000 años de tradición y nos entregó las claves para entender el cosmos.
El Misterio de los Cielos
Antes de los telescopios, antes de la luz eléctrica, el cielo nocturno era el mayor espectáculo del mundo. Noche tras noche, durante miles de años, la humanidad observó el mismo ballet cósmico. Las estrellas fijas giraban en una danza predecible, pero cinco "vagabundos" se negaban a seguir el guion. Mercurio, Venus, Marte, Júpiter y Saturno se movían de forma extraña, a veces incluso retrocediendo en el cielo. Eran los planetas, del griego "planētēs", que significa "errante".
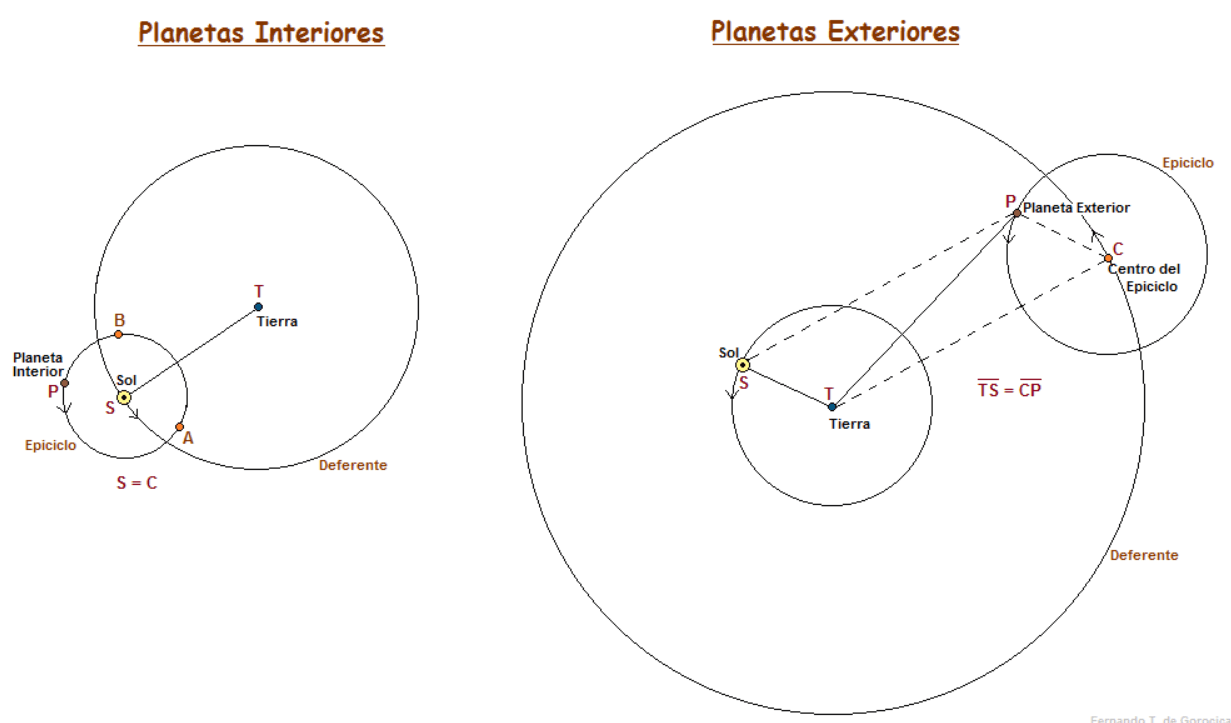
Para los antiguos, imbuidos de la filosofía de Platón y Aristóteles, el cosmos era el reino de la perfección divina. Y la forma geométrica más perfecta era el círculo. Por tanto, los planetas debían moverse en círculos perfectos. El problema es que las observaciones no encajaban.
Para salvar la idea del círculo, astrónomos como Ptolomeo crearon sistemas increíblemente complejos de "epiciclos": círculos que giraban sobre otros círculos. Era un parche matemático, un intento desesperado por forzar la realidad a encajar en una idea preconcebida. Durante casi 2.000 años, nadie se atrevió a desafiar la tiranía del círculo. Hasta que llegaron dos hombres que cambiarían la historia.
Tycho Brahe: El Señor de los Datos con Nariz de Metal
Nuestra historia comienza con uno de los personajes más excéntricos de la historia de la ciencia: Tycho Brahe. Un noble danés, duelista, astrónomo y, según se dice, dueño de un alce como mascota que murió al caer por las escaleras borracho. Tras perder parte de su nariz en un duelo por una disputa matemática, lució durante el resto de su vida una prótesis de latón y plata.
Pero su verdadera excentricidad era una obsesión fanática por la precisión. Convenció al rey de Dinamarca para que le financiara la construcción de Uraniborg, un castillo-observatorio en la isla de Hven. Equipado con los instrumentos más grandes y precisos jamás construidos, Tycho se dedicó durante más de 20 años a una tarea monumental: medir y registrar la posición de los planetas y las estrellas noche tras noche, con una precisión nunca antes vista. Y todo ello, sin telescopio.
Tycho no buscaba una nueva teoría. Creía en su propio modelo geo-heliocéntrico. Lo que él quería eran datos. Datos puros, duros e irrefutables. Sin saberlo, estaba forjando el arma que destruiría su propio universo. Estaba acumulando el oro que otro hombre usaría para desenterrar el verdadero secreto del cosmos.

Kepler: El Genio Atormentado que Heredó los Cielos
En 1600, un brillante y acosado matemático alemán llamado Johannes Kepler llegó a Praga. Su vida era un caos: como protestante, huía de la persecución religiosa, había perdido a su primera mujer y a varios de sus hijos, y a menudo vivía en la pobreza. Sin embargo, en medio del tormento, Kepler era un hombre de fe inquebrantable en un universo ordenado. Estaba convencido de que Dios era un geómetra y que había diseñado el cosmos según una armonía matemática perfecta que él estaba destinado a descubrir.
Llegó para ser el ayudante de Tycho, y la relación fue eléctrica desde el principio. Era el choque de dos mundos: el aristócrata observador contra el teórico plebeyo. Tycho, posesivo y celoso de sus datos, veía el genio de Kepler pero temía que le eclipsara. Por eso, le asignó el problema más endemoniado que tenía: descifrar la órbita de Marte, el planeta más rebelde, para mantenerlo ocupado y lejos del resto de su tesoro de datos. La tensión era palpable; Tycho le daba los datos a cuentagotas, lo justo para que trabajara, pero nunca el conjunto completo.
Cuando Tycho murió repentinamente en 1601, Kepler, en un acto de audacia, se hizo con el tesoro al completo: décadas de observaciones de valor incalculable. Fue entonces cuando comenzó su verdadera guerra.
La Batalla por 8 Minutos de Arco
Durante años, Kepler se sumergió en un infierno de cálculos. Intentó una y otra vez ajustar los datos de Marte a una órbita circular, el dogma de 2.000 años. Fracasó. Probó con excéntricos, epiciclos, todo el arsenal de la astronomía clásica. Nada funcionaba. Siempre quedaba una diferencia minúscula pero persistente, de apenas 8 minutos de arco (unos 0,13°).
Lo fácil habría sido rendirse. "Bah, un simple error de medición", podría haber pensado. Pero Kepler confiaba ciegamente en la exactitud casi sobrehumana de Tycho. Esa diferencia mínima le obsesionó porque sabía que no era ruido: si la naturaleza no coincidía con el modelo, el modelo estaba mal. Fue esa honestidad intelectual la que le llevó a cometer la mayor herejía de la astronomía: abandonar el círculo perfecto. Después de incontables páginas de cálculos y años de frustración, probó con la forma que los antiguos habían despreciado por "imperfecta": la elipse. Y de repente, como por arte de magia, todo encajó a la perfección. El momento "eureka" debió ser sobrecogedor, el alivio de un hombre que había luchado contra el cielo y, por fin, lo había entendido.
Él mismo escribió en su Astronomia Nova (1609): "Si hubiera despreciado esos 8 minutos de arco, habría tapado la física. Pero, como no debían ser despreciados, fue necesario abandonar los círculos y atreverse con la elipse."
La Primera Ley: Las Órbitas No Son Círculos, Son Elipses
El primer golpe de Kepler a la astronomía clásica fue demoledor. Su Primera Ley establece que todos los planetas se mueven en órbitas elípticas, con el Sol situado en uno de sus focos. Se acabó el círculo perfecto. Una elipse es una especie de círculo "aplastado" definido por dos puntos centrales llamados focos. El Sol no está en el centro, sino en uno de esos focos. Esto tiene una consecuencia clave: la distancia planeta-Sol varía constantemente.
Para la clase: La forma de una elipse se define por su excentricidad (e), un número entre 0 y 1. Si e=0, la elipse es un círculo perfecto y los dos focos coinciden en el centro. A medida que e aumenta, la elipse se vuelve más alargada. Los puntos de la órbita más cercano y más lejano al Sol se llaman perihelio y afelio, respectivamente.
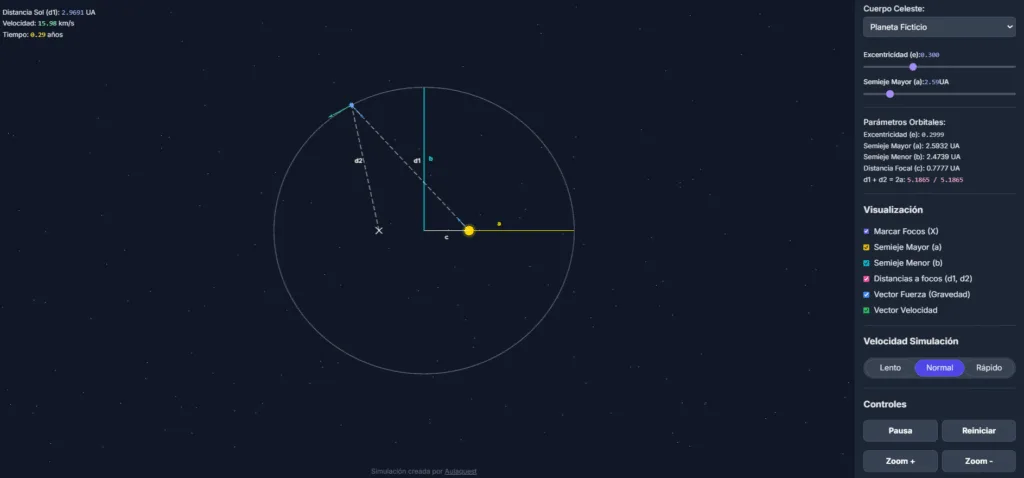
Dibuja tu Propia Órbita
¿Quieres ver cómo una pequeña variación en la excentricidad transforma un círculo en una elipse? En nuestro simulador, puedes manipular la órbita y comprobar visualmente la Primera Ley de Kepler.
La Segunda Ley: El Planeta Barrendero
La órbita elíptica implicaba algo más: los planetas no se mueven a velocidad constante. Su Segunda Ley, la ley de las áreas, lo explica de una forma bellísima: la línea que une un planeta con el Sol barre áreas iguales en tiempos iguales.
Imagina que el planeta es un barrendero cósmico. Cuando está más cerca del Sol (perihelio), se mueve más rápido, barriendo un sector ancho pero corto. Cuando está más lejos (afelio), se mueve más lento, barriendo un sector estrecho pero largo. Lo asombroso es que el área de ambos sectores es exactamente la misma si se miden en el mismo intervalo de tiempo.
Para la clase: Este fenómeno es una consecuencia directa de la conservación del momento angular (L). El momento angular ($L = m \cdot r \cdot v \cdot \sin(\theta)$) se mantiene constante en todo momento. Como la masa (m) no cambia, cuando la distancia al Sol (r) disminuye, la velocidad (v) debe aumentar para que el producto se mantenga, y viceversa. Por eso el planeta acelera en el perihelio y frena en el afelio.
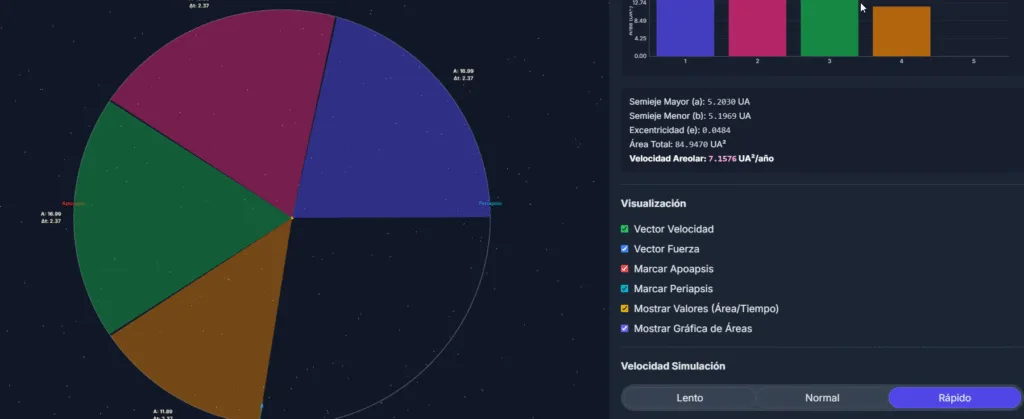
Activa el "Modo Barrendero"
Ver es entender. Nuestro simulador te permite visualizar las áreas barridas por el planeta en tiempo real y comprobar con tus propios ojos que, aunque la velocidad cambie, el área barrida por segundo es siempre constante.
La Tercera Ley: La Armonía de los Mundos
Diez años después, en 1619, Kepler encontró la joya de la corona, la ley que conectaba a todos los planetas en una única sinfonía matemática. Su Tercera Ley, o ley armónica, establece que el cuadrado del período orbital de un planeta es directamente proporcional al cubo de la longitud de su semieje mayor.
En lenguaje sencillo: los planetas más lejanos no solo tienen órbitas más grandes, sino que también se mueven mucho más lento. Pero lo hacen siguiendo una proporción matemática perfecta. Esta ley permite comparar las órbitas de diferentes planetas. Si conoces cuánto tarda un planeta en dar una vuelta al Sol, puedes saber a qué distancia media se encuentra. Era la armonía que Kepler había buscado toda su vida.
Fórmula de la 3ª Ley: $T^2 \propto a^3$ o $\frac{T^2}{a^3} = k$ (una constante para todos los planetas del sistema)
De Kepler a Newton: Del "Cómo" al "Porqué"
Las leyes de Kepler eran descriptivas. Nos decían con una precisión asombrosa cómo se movían los planetas, pero no por qué. Ese fue el trabajo de otro gigante: Isaac Newton. Medio siglo después, Newton tomó las leyes de Kepler y, con su Ley de la Gravitación Universal, proporcionó la explicación física que faltaba.
Newton postuló que todos los objetos del universo se atraen con una fuerza que es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. Utilizando esta ley y sus propias leyes del movimiento, fue capaz de derivar matemáticamente las tres leyes de Kepler. Demostró que las órbitas elípticas, la variación de la velocidad y la proporción armónica eran todas consecuencias inevitables de esta única y elegante fuerza universal. Kepler describió la danza; Newton reveló al bailarín invisible.
Ley de la Gravitación Universal: $F = G \frac{m_1 m_2}{r^2}$
Donde F es la fuerza de gravedad, G es la constante de gravitación universal, m₁ y m₂ son las masas de los dos cuerpos, y r es la distancia entre ellos.
¿Por Qué Nos Importa Kepler Hoy?
Las leyes de Kepler no son una reliquia histórica. Son la base de toda la mecánica orbital moderna. Cada vez que lanzamos un satélite, enviamos una sonda a Marte o calculamos la órbita de un cometa, estamos usando las mismas tres leyes que un matemático obstinado arrancó de los datos de un noble danés hace 400 años.
Su legado llega incluso a la caza de nuevos mundos. El famoso Telescopio Espacial Kepler de la NASA utilizó sus principios para descubrir miles de exoplanetas. ¿Cómo? Mediante el método de tránsito. El telescopio observaba fijamente más de 150.000 estrellas, buscando minúsculas y periódicas caídas en su brillo. Esa atenuación es la sombra de un planeta pasando por delante de su estrella, un "mini-eclipse". Al medir cuánto cae el brillo y cada cuánto tiempo ocurre, los astrónomos pueden deducir el tamaño del planeta y, usando la Tercera Ley de Kepler, la distancia a su estrella. De alguna manera, seguimos usando la geometría de Kepler para mapear la galaxia.
El GPS de tu móvil es otro ejemplo perfecto. Las órbitas de los 24 satélites que forman la constelación GPS se calculan con las leyes de Kepler y la gravedad de Newton. Sin embargo, para la increíble precisión que necesitamos, la física clásica no es suficiente. Los relojes atómicos de los satélites, al moverse a gran velocidad (efectos de la Relatividad Especial) y en un campo gravitatorio más débil (Relatividad General), se desajustan. Sin las correcciones de Einstein, el GPS acumularía errores de kilómetros en horas. Así, en tu bolsillo conviven el universo de Kepler, Newton y Einstein.
Fuentes y Bibliografía Recomendada
- Sagan, Carl. Cosmos. Un clásico indispensable que narra esta historia con una pasión inigualable.
- Ferguson, Kitty. Tycho y Kepler: El astrónomo excéntrico y el visionario que juntos revolucionaron la astronomía. Una biografía detallada de la fascinante relación entre ambos.
- Wikipedia: Artículos sobre Johannes Kepler, Tycho Brahe e Isaac Newton.
Conclusión: El Legado de la Obsesión
La historia de Kepler es un recordatorio de que la ciencia no avanza en línea recta. Es un camino tortuoso, lleno de ideas preconcebidas, tragedias personales y una lucha constante contra el dogma. Se necesitó la obsesión de Tycho por los datos y la obstinación de Kepler por la verdad para romper con dos milenios de pensamiento. Nos enseñaron que las ideas más bellas deben rendirse ante la evidencia, incluso si esa evidencia es tan pequeña como 8 minutos de arco en el cielo nocturno.
Hoy, no necesitas pasar una década haciendo cálculos para revivir ese descubrimiento. Puedes experimentar con las órbitas, cambiar los planetas y verificar las leyes por ti mismo. Te invitamos a descubrir cómo se mueven los planetas y a sentir, por un momento, el asombro que sintió Kepler cuando las piezas del puzle cósmico por fin encajaron.
Conviértete en un Astrónomo
Descubre tú mismo cómo se mueven los planetas, verifica las tres leyes y crea tu propio sistema solar con nuestras simulaciones interactivas.
¿Cansado de que tus Alumnos Vean las Órbitas como Dibujos Planos?
Sabemos que enseñar mecánica orbital en una pizarra es un reto. Las fórmulas son abstractas y la dinámica, difícil de imaginar. Con AulaQuest, pasas de la explicación estática a la experimentación dinámica. Dales un sistema solar de bolsillo y verás cómo su comprensión (y su interés) se dispara.