Simulador de Efecto Fotoeléctrico

⚡ ¿Más luz = más electrones?

Eso creían los físicos… hasta que vieron que, a veces, ni con mil focos salía uno.

Con este simulador de Efecto Fotoeléctrico vas a descubrir por qué Einstein rompió las reglas y qué tiene que ver la frecuencia con todo esto.

📋 Detalles de la simulación

🔗 Categoría: Física ↗️
🎓 Nivel educativo: Bachillerato
⚙️ Dificultad: Media
📈 Visitas: 31

📎 Código para incrustar

¿Eres profe, divulgador o webmaster?
Puedes incrustar esta simulación en tu web o blog sin problema.

Solo pedimos dos cosas básicas:

✅ Que cites la fuente: AulaQuest.com
🚫 Que no la uses con fines comerciales

Este es el código que puedes copiar:

<iframe
  src="https://aulaquest.github.io/efecto-fotoelectrico/"
  width="100%"
  height="560"
  style="border: 1px solid #ccc; border-radius: 8px;"
  allowfullscreen
  title="Simulación Efecto Fotoeléctrico"></iframe>

Introducción al Efecto Fotoeléctrico

Hola. Hoy nos metemos de lleno con un fenómeno que la verdad cambió bastante cómo entendíamos la luz y la materia. Hablamos del efecto fotoeléctrico. Efectivamente. Que además es algo que se puede ver muy bien, ¿eh?, con la simulación que tenemos delante.

O sea, imagínate, apuntas con luz a un metal y zas, empiezan a saltar electrones. Sí, se genera una corriente. Parece casi magia, pero no, no,

es física pura y dura, y de la interesante. Totalmente. Es un proceso donde la luz interactúa con los electrones de un material de una forma, bueno, muy particular.

Vamos a ver qué factores influyen ahí, ¿no? Y cómo se relacionan. Sobre todo pensando en cómo manejar la simulación para entenderlo bien. Vale. La idea es entender qué controla esta interacción luz-materia a este nivel.

Perfecto. Pues, eh, vamos a ello. Tenemos las descripciones del efecto y la propia simulación para experimentar. Veremos cómo la energía de la luz, el tipo de metal que elijamos

y otros ajustes que podemos tocar, Sí. pues cómo afectan a si los electrones se liberan o no y con qué energía salen. Si te parece, empezamos por lo más básico.

¿Qué pasa ahí exactamente? Pues mira, lo fundamental es que la luz, al darle a ciertos metales, puede arrancar electrones de su superficie. Vale.

Y eso genera la corriente eléctrica que comentábamos. Pero lo curioso, y aquí es donde la física clásica se quedó un poco pillada, ¿no? Ajá. Es que no servía cualquier tipo de luz.

Podías estar iluminando un metal con una luz superintensa durante horas, pero si no era de la frecuencia adecuada, pues nada. Nada de nada. Ni un electrón.

Ni uno. Cero. Y eso era un misterio tremendo en su momento.

La Naturaleza Cuántica de la Luz: Fotones

Claro, y ahí es donde entra la idea esta genial de que la luz no es una onda continua y ya está, sino que viene como en paquetitos. Justo. Como en paquetes discretos de energía.

Se llaman fotones. Fotones. Y cada fotón lleva una cantidad de energía muy concreta, que depende de su frecuencia ($f$), o si lo prefieres, de su longitud de onda ($\lambda$).

La lambda, que es lo que movemos en el simulador. Ah, vale, la barrita esa que deslizamos. Esa misma.

Energía del Fotón y Constante de Planck

La relación es: $$E = hf = \frac{hc}{\lambda}$$ Donde $h$ es la constante de Planck, un número clave en cuántica, y $c$ la velocidad de la luz. La de siempre. La de siempre.

Para la simulación, lo importante es si bajas la longitud de onda lambda ($\lambda$), aumentas la energía de cada fotón individual. Entendido. Menos lambda, fotones como más energéticos, más potentes.

¿Y el metal? Porque veo que en la simulación podemos cambiar de sodio a zinc, a litio... Claro, porque no todos los metales sueltan sus electrones igual de fácil.

Cada uno tiene como una especie de barrera de energía que hay que superar. Ajá.

La Función de Trabajo ($\phi$)

A eso se le llama la función de trabajo. Se representa con la letra griega phi: $$ \phi $$ Es la energía mínima, mínima que necesita un fotón para poder arrancar un electrón de ese metal en particular.

O sea, cada metal tiene la suya. Cada uno la suya, sí. Se suele medir en electronvoltios (eV), que es una unidad de energía pequeñita, muy útil a esta escala.

Por ejemplo, el litio que mencionabas tiene una función de trabajo de unos 2,9 eV. Vale.

Condición para la Emisión de Electrones

Pues si la energía del fotón que llega, que es $E_{fotón} = \frac{hc}{\lambda}$, es menor que esos 2,9 eV... Aunque mandes muchísimos fotones... Da igual cuántos mandes.

Si individualmente no tienen energía suficiente ($E_{fotón} < \phi$), no se libera ni un solo electrón. Cero corriente. Es como una llave, ¿no? Si no es la llave correcta para esa cerradura (la función de trabajo), no abres.

Exactamente. Esa es la idea. Pero, ¿y si la energía del fotón sí es mayor que phi? $$ E_{fotón} > \phi $$ Ah, entonces sí que saltan los electrones. ¡Bingo!

Energía Cinética de los Fotoelectrones ($KE_{max}$)

El electrón se libera. Y además, la energía que le sobra al fotón, después de superar esa barrera $\phi$... ¿Qué pasa con ella? Se convierte en la energía de movimiento del electrón.

Es su energía cinética máxima, la $KE_{max}$. Ah, claro. La fórmula es sencilla: $$ KE_{max} = E_{fotón} - \phi = \frac{hc}{\lambda} - \phi $$

Por eso, si en la simulación usas longitudes de onda más cortas (o sea, fotones con más energía)... Veremos electrones saliendo más rápido. Justo. No solo salen,

sino que salen disparados con más velocidad, con más $KE_{max}$. Se ve perfectamente en la animación. Vale, vale. Captado.

Influencia de la Intensidad de la Luz

La energía del fotón es crucial, depende de lambda ($\lambda$). Pero, ¿qué pasa con la intensidad de la luz? Si ya estoy usando una luz buena, con energía por encima de $\phi$, y ahora subo la intensidad en el simulador, ¿qué cambia?

Buena pregunta, porque ahí la intuición también nos puede jugar malas pasadas. Aumentar la intensidad, cuando ya estás por encima de esa energía umbral $\phi$, Sí.

lo que significa es que estás mandando más fotones cada segundo. Pero ojo. ¿Qué? Cada uno de esos fotones sigue teniendo exactamente la misma energía individual que antes.

La intensidad no cambia la energía de cada fotón. Ah, vale. Entonces, como cada fotón con energía suficiente libera un electrón, si mandas más fotones...

Liberas más electrones por segundo. Exacto. Y más electrones por segundo significa... Más corriente eléctrica. Lo que mide el amperímetro en la simulación. Eso es.

El amperímetro sube, pero, y eso es importante, si la energía de cada fotón no era suficiente para empezar, estaba por debajo de $\phi$, ya puedes subir la intensidad todo lo que quieras.

Que no sirve de nada. Más fotones inútiles no consiguen nada. La corriente sigue siendo cero patatero. Clarísimo.

Intensidad es cantidad de fotones, no calidad energética de cada uno.

Potencial de Frenado ($V_0$)

Oye, ¿y el voltaje ese negativo que se puede aplicar, que parece que frena a los electrones? Sí. Eso es el potencial de frenado ($V_0$). Es como ponerles un freno eléctrico.

¿Cómo funciona? Pues aplicas un voltaje negativo en la placa que recoge los electrones. Eso crea un campo eléctrico que los repele, que los frena.

Si vas subiendo ese voltaje negativo... Los frenas cada vez más. Correcto. Hasta que llegas a un punto en que frenas incluso a los más rápidos, a los que salieron con la $KE_{max}$.

Y la corriente se hace cero. Exacto. Ese valor de voltaje justo que anula la corriente es el potencial de frenado. Y está directamente relacionado con la energía cinética máxima: $$ KE_{max} = e V_0 $$

Donde $e$ es la carga del electrón. De hecho, $KE_{max}$ es igual a la carga del electrón multiplicada por ese potencial de frenado. Es una forma de medir esa $KE_{max}$ indirectamente. Vaya.

Resumen y Conexión con la Naturaleza Corpuscular de la Luz

O sea que todo este lío se explica pensando en la luz como si fueran partículas, fotones, chocando y pasando energía. Básicamente sí.

Una idea que parece simple ahora, pero que fue super revolucionaria. Le valió el Nobel a Einstein, ¿no? Ni más ni menos. Fue un paso clave

para abrir la puerta a la física cuántica. A entender que el mundo a escala muy pequeña funciona con otras reglas. Y pensar que esto mismo está pasando en las placas solares, por ejemplo.

Exactamente.

Conclusiones Clave de la Simulación

Al final, todo se reduce a comparar la energía que trae cada fotón (que en la simulación controlas con $\lambda$), con la energía mínima que necesita el metal para soltar un electrón, su función de trabajo $\phi$.

Si gana el fotón ($E_{fotón} > \phi$), sale el electrón. Y la energía que sobra se la lleva el electrón como energía cinética ($K_{max}$).

La intensidad solo dice cuántos fotones ganadores llegan por segundo. Mmm. Por eso, jugar con la simulación es genial para pillar estas relaciones.

Cambias $\lambda$, ves qué pasa con la energía y la $K_{max}$. Cambias el material, ves cómo afecta $\phi$. Subes la intensidad, ves cómo sube la corriente.

Pero no la energía de cada electrón. Pues sí, la verdad es que ahora queda mucho más claro cómo funciona y qué esperar al tocar cada control en la simulación.

Pregunta Final: Dualidad Onda-Partícula

Y bueno, para dejar algo en el aire mientras se experimenta. Si la luz, que siempre pensamos como una onda, aquí se comporta como partículas, como fotones. Ajá.

¿Podría ser al revés? ¿Podrían las partículas, como los propios electrones, comportarse a veces como si fueran ondas? Ahí lo dejo.

Mmm, interesante pregunta para darle vueltas. Sí, señor.

¿Qué es el efecto fotoeléctrico?

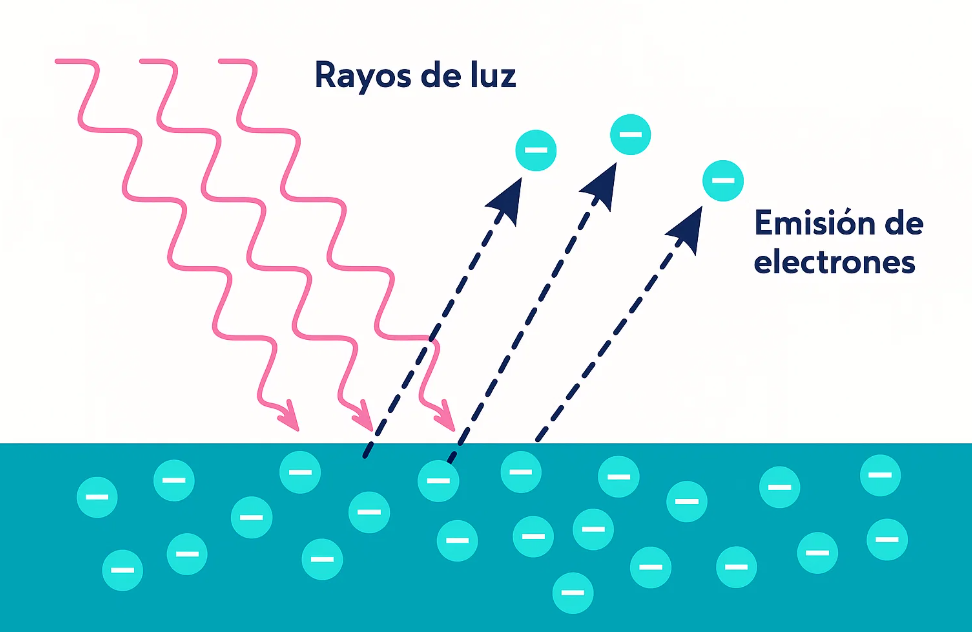
Imagina que apuntas con luz a un metal y, ¡zas!, empiezan a saltar electrones y a generar corriente. Parece magia, pero en realidad es física cuántica en acción. El efecto fotoeléctrico consiste precisamente en eso: en la emisión de electrones por un material al ser iluminado con luz de la energía adecuada.

Lo desconcertante —al menos para la física clásica— es que no vale cualquier luz. La explicación revolucionaria de Einstein fue que la luz no es una onda continua, sino que está formada por paquetes de energía llamados fotones.

Ilustración del efecto fotoeléctrico mostrando fotones liberando electrones de un metal.

Ilustración del efecto fotoeléctrico: cada fotón interactúa con un electrón.

La Función de Trabajo (φ): La "llave" de cada metal

No todos los metales sueltan sus electrones con la misma facilidad. Cada material tiene una barrera de energía que hay que superar, una especie de "peaje" que el fotón debe pagar para liberar al electrón.

Esta energía mínima se llama Función de Trabajo y se representa con la letra griega phi ($\varphi$). Es como la cerradura de una puerta: necesitas la llave correcta para abrirla.

Cada material que eliges en la simulación (Sodio, Potasio, Platino...) tiene su propia función de trabajo $\varphi$, medida en electronvoltios (eV), una unidad de energía muy útil a esta escala.

La Energía del Fotón (E): La "fuerza" de la llave

La energía de cada fotón (la "fuerza" de la llave) depende de su longitud de onda ($\lambda$), que es el control que mueves en la simulación. La relación es inversa:

$ E_{\text{fotón}} = \frac{h \cdot c}{\lambda} $

E: Energía del fotón (en eV).
λ: Longitud de onda de la luz (en nm). Es la barra que deslizas.
h: Constante de Planck ($4.136 \times 10^{-15} \text{ eV·s}$).
c: Velocidad de la luz ($3 \times 10^8 \text{ m/s}$).

En la simulación, esto es clave: al disminuir la longitud de onda λ, creas fotones más energéticos y "potentes".

La Condición: ¿Cuándo saltan los electrones?

Un electrón solo será liberado si la energía del fotón que impacta es mayor o igual que la función de trabajo del metal. Es una batalla uno contra uno:

$ E_{\text{fotón}} \ge \varphi $

Si la energía del fotón no es suficiente ($E_{\text{fotón}} < \varphi$), no pasa nada. Puedes mandar millones de fotones "débiles", que la corriente será cero patatero. Si la energía es suficiente, ¡bingo!, el electrón salta.

La longitud de onda umbral ($\lambda_0$) es la longitud de onda máxima que justo consigue liberar electrones. Cualquier valor por encima de $\lambda_0$ no funcionará.

La Energía que "sobra": Energía Cinética ($K_E$)

Cuando el fotón tiene más energía de la necesaria, la energía que "sobra" tras pagar el peaje ($\varphi$) no se pierde. Se convierte en la energía de movimiento del electrón, es decir, su energía cinética máxima ($K_{E, \text{máx}}$).

Por eso, los electrones no solo escapan, ¡salen disparados! La famosa ecuación de Einstein lo resume:

$ K_{E, \text{máx}} = E_{\text{fotón}} - \varphi = \frac{h \cdot c}{\lambda} - \varphi $

Esto significa que cuanto más corta sea la longitud de onda ($\lambda$), mayor será la energía del fotón y, por tanto, más rápido saldrán los electrones. Lo verás claramente en la animación.

¿Y la Intensidad de la Luz?

Aquí la intuición puede fallar. Aumentar la intensidad de la luz NO cambia la energía de cada fotón. La intensidad se refiere al número de fotones que llegan por segundo.

Si la luz es "eficaz" ($E_{\text{fotón}} > \varphi$): Al subir la intensidad, mandas más fotones "ganadores". Cada uno libera un electrón, por lo que la corriente eléctrica aumenta.
Si la luz NO es "eficaz" ($E_{\text{fotón}} < \varphi$): Puedes subir la intensidad al máximo. Solo estarás mandando más fotones "inútiles". La corriente seguirá siendo cero.

En resumen: Intensidad es CANTIDAD de fotones, no CALIDAD (energía) de cada uno.

El Potencial de Frenado: ¿Cómo medir su energía?

El potencial de frenado ($V_0$) es un truco para medir la energía cinética de los electrones. Es un voltaje negativo que aplicas para "ponerles un freno eléctrico".

Al ir aumentando este voltaje negativo, frenas a más y más electrones hasta que, en un punto exacto, detienes incluso a los más rápidos. En ese momento, la corriente se hace cero. Este valor de voltaje nos permite calcular la energía cinética máxima:

$ K_{E, \text{máx}} = e \cdot V_0 $

Donde e es la carga del electrón. Es una forma ingeniosa de medir la energía de los electrones sin tener que cronometrarlos.

Resumen para la Simulación

Antes de empezar a experimentar, ten estas ideas claras:

La Longitud de Onda ($\lambda$) controla la ENERGÍA de cada fotón. Menos $\lambda$, más energía.
El Material que eliges determina la FUNCIÓN DE TRABAJO ($\varphi$), la barrera a superar.
La Intensidad controla la CANTIDAD de fotones que llegan por segundo.
El Voltaje de Frenado ($V_0$) te permite MEDIR la energía cinética de los electrones.

Esta no es solo una simulación. Es un laboratorio cuántico al alcance de tu clic. ¡A experimentar!

¿Has entendido de verdad el efecto fotoeléctrico?

Has explorado la simulación. Has escuchado (o leído) el PodQuest. Has revisado la teoría paso a paso. Ahora es el momento de poner en práctica lo aprendido: ¿realmente has comprendido los conceptos?

A continuación encontrarás una actividad de repaso diseñada para ayudarte a aplicar tus conocimientos utilizando la simulación.

Esta actividad está pensada como parte de una dinámica de aula, pero también puede realizarse de forma individual. Los ejercicios están organizados por bloques, y no es necesario completar ni enviar todos. El profesor puede decidir con cuáles trabajar en función de los objetivos de la sesión.

Lo importante es que respondas con atención. Tus respuestas le ayudarán al profesor a valorar tu progreso... y a ti, a saber si has comprendido de verdad los conceptos o si necesitas repasarlos un poco más.

🧪 Parte 1: ¿Puede esta luz arrancar electrones?

Condiciones iniciales: Material: Potasio

Longitud de onda: 540 nm
Intensidad: 50%
Voltaje: 0.00 V

1.Observa lo que ocurre con esos valores. ¿Se produce corriente? ¿Por qué crees que sucede esto?

2. Reduce la longitud de onda poco a poco (por ejemplo a 520 nm, 500 nm, 480 nm…).

¿Cuál es la longitud de onda más grande (λ) que todavía permite la emisión de electrones en el potasio?

3. Compara ahora con otros materiales.

¿Qué material permite arrancar electrones con la longitud de onda más larga?

Sodio (Na)
Cesio(Cs)
Uranio(U)
Platino(pt)

4. Encuentra la longitud de onda mínima que permite arrancar electrones en cada material.

Usando el simulador, reduce poco a poco la longitud de onda para cada uno de estos materiales (K, Ca, U) hasta encontrar el valor más largo (λ máxima) que todavía permite la emisión de electrones (es decir, donde la corriente deja de ser cero).

Calcula la frecuencia $f = \frac{c}{\lambda}$ y luego la energía del fotón $E = h \cdot f$. Usa:

$h = 4.136 \times 10^{-15} \, \text{eV·s}$
$c = 3 \times 10^8 \, \text{m/s}$

Elementos a investigar: Potasio (K), Calcio (Ca) y Uranio (U)

Elemento	Longitud de onda máxima (nm)	Frecuencia (Hz)	Energía del fotón (eV)

⚡ Parte 2: Cambios en la intensidad de luz

5. Elemento: cesio, longitud de Onda 400nm.

Prueba con intensidad 10%, 50% y 100%. ¿Qué observas en la corriente eléctrica generada?

¿La energía de los electrones cambia también?

6. ¿Cuál de estas afirmaciones es cierta según tu experimento?

(Se puede marcar mas de una opción)

A mayor intensidad mayor energía de los electrones
A mayor intensidad más electrones son arrancados pero su energía no cambia
La intensidad afecta solo a la velocidad de los electrones

🔋 Parte 3: Explorando el voltaje de frenado

Usa longitud de onda = 300 nm, intensidad = 100%, material Uranio

7. Disminuye el voltaje de forma progresiva desde 0 V hasta que dejen de llegar electrones al amperímetro.
¿Cuál es el voltaje que permite el paso de electrones?

8. Este valor corresponde a la energía cinética máxima de los electrones emitidos. ¿Cuánto vale?

9. ¿Por qué crees que la energía cinética máxima no cambia aunque varies el voltaje?

🧬 Parte 4: Explorando la tabla periódica y la función de trabajo

En general, la dificultad para arrancar electrones aumenta de izquierda a derecha en cada periodo de la tabla periódica. Busca en la tabla periódica potasio (K), calcio (Ca) y uranio (U).

10. Basándote en sus posiciones, indica cuál de ellos tendrá una función de trabajo más baja y cuál más alta:

Menor función de trabajo	Mayor función de trabajo:

11. Basándote en los resultados obtenidos en la tabla, explica cuál de ellos retiene más fuertemente sus electrones.

Instrucciones para enviar tus respuestas al profe

Completa las actividades que te haya indicado tu profe.
Haz clic en “Revisar y enviar al profe”.
Revisa tus respuestas. Si necesitas corregir algo, pulsa “❌ Corregir”.
Cuando estén bien, haz clic en “📋 Copiar respuestas”.
Luego pulsa “📬 Abrir Gmail” y pega las respuestas en el correo.
Escribe el asunto y el email del profe, y pulsa Enviar.

En AulaQuest no se guarda nada. Tus respuestas no se almacenan, no se asocian a tu cuenta y nadie más las verá. Es solo un canal directo y privado entre tú y tu profe.

Soluciones de las actividades Propuestas

📚 Zona Profe – Acceso exclusivo para docentes

Bienvenido a la Zona Profe. Aquí encontrarás las soluciones detalladas de las actividades propuestas para tus estudiantes. Cada una ha sido elaborada con rigor y cuidado, basándonos en los datos del simulador y principios físicos sólidos.

Eso sí, aunque revisamos todo con atención, puede colarse alguna imprecisión. Te recomendamos que, antes de usar estas soluciones para corregir o explicar en clase, verifiques los cálculos por si acaso. Gracias por tu confianza y por hacer de la ciencia algo emocionante.

🔒 Esta solución está disponible solo para docentes registrados.

¿Eres profe? Solicita acceso aquí para desbloquear los recursos exclusivos.

Actividades enviadas por maestros

ac¡tividad 2 de paco

👨‍🏫 Profesor: Jose Luis Bernal

🏫 Centro: I.E.P Ategorri

🔍 Ver actividad

activida de paco