Simulador de Modos normales y Oscilaciones Forzadas

🎼 Laboratorio online de Modos Normales y Resonancia

Comprender las oscilaciones es esencial en física. En este laboratorio virtual podrás explorar modos normales, analizar oscilaciones forzadas, identificar la resonancia y visualizar batidos con gráficos interactivos.

Ajusta parámetros y observa cómo evoluciona la dinámica de los sistemas acoplados.

  • 🔗 Categoría: Física | Ondas y sonido ↗️
  • 🎓 Nivel educativo: Universidad
  • ⚙️ Dificultad: Media (6/10)
  • 📈 Visitas: 52
Nivel educativo Universidad
Dificultad Media (6/10)
Visitas 52
Pantalla Completa
Pantalla Completa

Introducción a las Oscilaciones y Ondas

Hola, iniciamos hoy una exploración del fascinante mundo de las oscilaciones y las ondas.
Tenemos delante una herramienta de simulación increíble, muy usada en entornos como Aula Quest, que permite ver la física, bueno, verla en acción.
Para quienes puedan tenerla abierta ahora mismo, será una oportunidad genial para experimentar en directo.
Exacto. La idea es usar esta visualización para desentrañar juntos conceptos clave: modos normales, superposición, batidos, resonancia.
Vamos a ver cómo se comportan estos sistemas de masas y resortes.

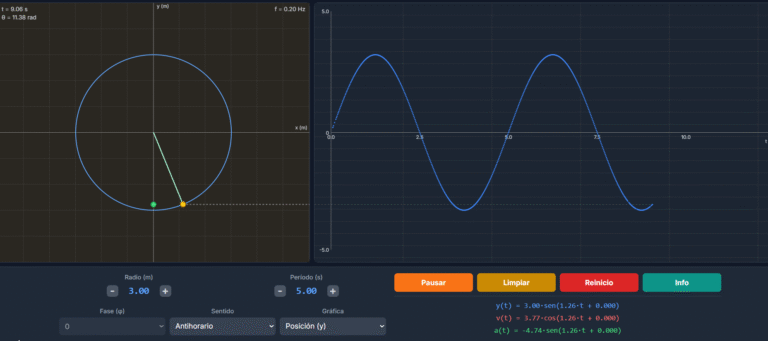
El Oscilador Armónico Simple: La Base de Todo

Pues manos a la obra, o mejor dicho, a los controles del simulador. Empezaremos por lo más sencillo para, bueno, para ir cogiendo confianza.
Siguiendo la guía de exploración, lo primero es simplificar al máximo. Reduzcamos el sistema a una sola masa usando el botón menos. A ver... ya está.
Lo que tenemos ahora es la base de todo: un oscilador armónico simple. Una única masa unida a dos resortes.
En el modo de simulación "real", si arrastramos la masa un poco hacia un lado y la soltamos, ¿qué vemos?
Un movimiento muy limpio, periódico, ¿verdad? Va y viene de forma constante.
Justo, es la clásica oscilación senoidal. Este es el comportamiento, digamos, fundamental. Define una frecuencia natural, la manera intrínseca en que este sistema simple prefiere vibrar si se le deja solo.
Podríamos decir que es como su huella dactilar vibratoria.

Conservación de la Energía

El panel de control solo aparece un modo de vibración listado. Esa es su única frecuencia natural. Muy claro, sí.
Volvamos al modo "real". Si ponemos la masa en movimiento otra vez y activamos la gráfica energía-tiempo, ah, asegurándonos de que el amortiguamiento B está a cero, observamos la línea blanca de la energía total, T. Es completamente plana, ¿no? Horizontal.
Precisamente. Es una ilustración perfecta de la conservación de la energía mecánica en un sistema idealizado, sin rozamiento. Vemos cómo la energía cinética K (naranja), asociada al movimiento, y la energía potencial elástica P (azul), bueno, la que está almacenada en los resortes, fluctúan constantemente.
Una sube mientras la otra baja. Se intercambian papeles, pero la suma total no cambia.

La Frecuencia Doble de la Energía

Ah, vale. Exacto. Y aquí hay un detalle, fíjate, que a menudo pasa desapercibido al leerlo pero que la gráfica muestra muy bien. Fíjate en la rapidez de las oscilaciones de K y P. ¿Ves que completan su ciclo dos veces por cada ciclo completo de vaivén de la masa?
Ostras, es verdad, suben y bajan el doble de rápido que la posición. ¿Y eso por qué?
Porque ambas energías dependen del cuadrado de una magnitud. La potencial depende del cuadrado de la posición, $$x^2$$.
Ajá. Y la cinética, del cuadrado de la velocidad, $$v^2$$. Al depender del cuadrado, da igual si la masa está a la derecha o a la izquierda, o si se mueve a la derecha o izquierda; la energía es positiva.
¡Ah, claro! Por eso, el ciclo energético se completa más rápido, dos veces por cada oscilación completa de la masa. Es una de esas visualizaciones que aclaran mucho.
Entendido. Sí, sí, verlo así ayuda bastante.

Sistemas Acoplados y Modos Normales

Bueno, ya dominamos el caso simple. ¿Qué pasa si añadimos complejidad? Usemos el botón "plus" para poner dos masas. Si repetimos el proceso en modo "real", moviendo una de las masas, la cosa cambia. El movimiento ya no es tan... tan simple y puro, ¿no? Se ve más enrevesado.
Correcto. El movimiento se vuelve más intrincado, y la razón se ve si cambiamos al modo "normal". Ahora, el panel nos muestra dos modos normales distintos. Cada uno con su propia frecuencia característica.
Lo que observábamos antes en "real" al mover una masa así, de forma arbitraria, era en realidad una combinación, una superposición de estos dos modos fundamentales.
O sea, que al tocar una masa hemos activado, digamos, ambos modos a la vez, y lo que vemos es la mezcla.
Exactamente. Hemos entrado en el terreno de las oscilaciones acopladas. El movimiento de una masa influye en la otra a través del resorte que las conecta, y el sistema como un todo tiene ahora múltiples formas preferidas de vibrar.
Vale, esto empieza a parecerse más a cómo vibran las cosas en la realidad, ¿no? Con varios movimientos superpuestos.
Para entenderlo mejor, parece crucial manejar bien los distintos modos de visualización que ofrece el simulador.

Los Tres Modos de Visualización

Totalmente de acuerdo. Entender las tres vistas principales, "real", "normal" y "superposición", es clave. Son como distintas lentes que nos permiten analizar el mismo fenómeno físico desde ángulos diferentes.
El modo "real" simula la física completa, cómo se comportaría el sistema si lo pusiéramos en marcha en un laboratorio. Bueno, uno ideal, sin fricciones externas. Como vimos, si excitamos una sola masa en un sistema de varias, el movimiento resultante es complejo, porque de forma natural se activan simultáneamente varios modos normales. Es la respuesta global, digamos, espontánea del sistema.
El modo "normal", en cambio, nos ofrece una visión analítica, descompuesta. Nos muestra cada uno de los patrones puros de oscilación del sistema por separado. Cada uno de estos patrones o modos normales vibra a una frecuencia específica y única. Estas frecuencias no son aleatorias, ¿eh? Dependen de las propiedades del sistema: la masa m, la rigidez k, el número de masas N. Hay una fórmula matemática que las define. $$ \omega_n = f(m, k, N) $$ Pero lo importante es entender que cada modo es un patrón de vibración puro con su propia frecuencia natural. Es una herramienta de aprendizaje para aislar y comprender los modos, los ingredientes del movimiento complejo.
Interesante. Entonces, si seleccionamos ahora el modo "normal", podemos ver esos ingredientes puros. En el panel aparecen listados los modos con sus frecuencias. Si hacemos clic en el primero... mira, todas las masas se mueven al unísono, siguiendo un patrón muy definido. Si elegimos el segundo, ahora el patrón es diferente. Quizás los extremos se mueven en oposición al centro. Animo a quien esté siguiendo con el simulador a explorar los distintos modos para sistemas con más masas. Los patrones se vuelven más complejos, claro.
Y la tercera lente es el modo "superposición". Aquí, nosotros tomamos el control creativo. Nos permite construir una vibración compleja a medida, sumando manualmente los modos normales que queramos. Podemos elegir qué modos incluir, con qué intensidad (o sea, amplitud) y cómo empiezan (la fase). Es como ser un diseñador de ondas.
Me gusta esa idea. Entonces, resumiendo: "normal" nos muestra las piezas básicas del puzle vibratorio.
Eso es. "Superposición" nos permite construir con esas piezas como queramos.
Exacto. Y "real" nos enseña cómo esas piezas se combinan de forma natural cuando el sistema se mueve y vibra libremente. Es una forma muy potente de entender jugando, ¿no?
Muy potente, sí.

Ondas Transversales vs. Longitudinales

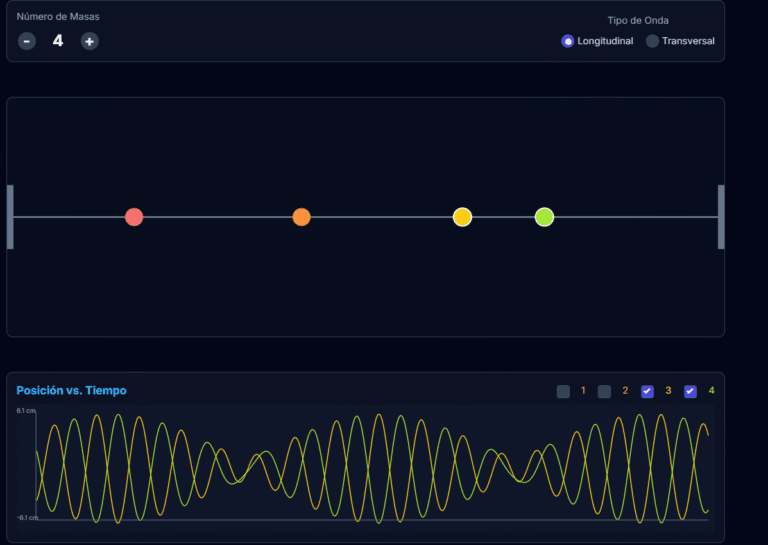
Ahora que manejamos los modos, hablemos de una distinción importante que el simulador ilustra muy bien: la diferencia entre ondas transversales y longitudinales.
En una onda transversal, las partículas del medio (en nuestro caso, las masas) oscilan en una dirección perpendicular a la dirección en la que se propaga la energía de la onda. El ejemplo típico es una ola en una cuerda de guitarra. La cuerda sube y baja, pero la onda viaja a lo largo de la cuerda.
Justo. En cambio, en una onda longitudinal, las partículas oscilan en la misma dirección (o sea, paralela) a la que viaja la onda. El sonido en el aire es el ejemplo clásico. Son compresiones y expansiones del aire que viajan en la dirección del sonido. Las partículas de aire vibran hacia adelante y hacia atrás en la misma línea.
Eso es. Vamos a verlo. Pongamos unas cuatro o cinco masas y volvamos al modo "real". Arriba podemos seleccionar el tipo de onda. Primero, transversal. Si ahora movemos una masa del extremo hacia arriba o abajo y la soltamos, observemos cómo esa perturbación, ese pico o valle, viaja a lo largo de la cadena. Las masas individuales suben y bajan, pero la onda avanza horizontalmente.
Se ve perfectamente. Clarísimo.
Ahora, cambiemos la opción a longitudinal. Hacemos lo mismo: movemos la masa del extremo, pero esta vez hacia la izquierda o la derecha, comprimiendo o estirando el primer resorte. ¿Qué ocurre? Vemos viajar una zona de compresión o expansión a lo largo de la cadena. Las masas se mueven horizontalmente y la onda también viaja horizontalmente.
Lo verdaderamente interesante aquí, y que el simulador deja patente, es lo que ambos tipos de onda tienen en común, a pesar de su apariencia distinta. En los dos casos, lo que viaja de un extremo a otro es energía, transmitida a través de la interacción entre las masas y los resortes. Pero, y esto es crucial, las masas individuales no viajan con la onda. Cada masa simplemente oscila alrededor de su posición de equilibrio.
O sea, la ola viaja, pero el agua (las partículas) no viaja con ella, solo sube y baja.
Mhm. O el sonido viaja, pero el aire no se desplaza en bloque, solo vibra localmente.
Exactamente. Y como la física subyacente depende de las propiedades del sistema (masas m, constantes elásticas k), que son las mismas en ambos casos, resulta que ambos tipos de onda comparten los mismos modos normales y las mismas frecuencias naturales.
¡Ah, qué curioso! Sí, y ambos pueden exhibir fenómenos como la resonancia. La única diferencia real es la dirección del movimiento de las partículas respecto a la dirección de propagación de la energía.

Fenómeno de Batidos o Pulsaciones

Ya que hemos hablado de modos normales y superposición, podemos explorar dos fenómenos muy interesantes que surgen de combinar ondas. El primero son los batidos, a veces llamados pulsaciones. Ocurren cuando se superponen dos ondas cuyas frecuencias son muy, muy parecidas, o sea, $$ \omega_1 \approx \omega_2 $$ El resultado no es simplemente una frecuencia intermedia, sino algo más complejo.
¿Qué es lo que vemos exactamente?
Vemos una onda que parece tener una frecuencia alta, cercana a las originales, pero cuya amplitud total no es constante, sino que aumenta y disminuye periódicamente, como si latiera.
Anda. Vamos a generarlos. En el modo "superposición" hay una opción muy cómoda: "Generar Batidos". Si la pulsamos, el simulador selecciona automáticamente los dos modos normales del sistema cuyas frecuencias estén más próximas entre sí y los activa.
Vale. Y para visualizarlo bien, activemos la gráfica posición-tiempo de una de las masas (la del centro suele dar una buena vista) y pulsemos play.
Es muy claro. Se ve la oscilación rápida, pero envuelta en una oscilación mucho más lenta de la amplitud. Esa variación lenta de la amplitud es el batido.
Justo de eso. Es interesante probar a superponer manualmente modos con frecuencias muy distintas. Veremos que este efecto de batido no aparece tan claramente. Se necesita que sean parecidas.

El Fenómeno de la Resonancia

Efectivamente, requiere frecuencias similares. El segundo fenómeno clave es la resonancia. Esto ocurre en un contexto diferente: cuando aplicamos una fuerza externa que varía periódicamente en el tiempo sobre nuestro sistema oscilante.
Si la frecuencia de esta fuerza impulsora, llamémosla $$\omega_d$$, coincide o está muy cerca de una de las frecuencias naturales del sistema, una de las $$\omega_n$$ de los modos normales, algo especial sucede, ¿no?
Pasa algo gordo. Sí. La transferencia de energía desde la fuerza externa hacia el sistema oscilante se vuelve extremadamente eficiente. El sistema absorbe energía muy fácilmente a esa frecuencia particular.
Y el resultado visible es...
un aumento muy grande, a veces espectacular, de la amplitud de las oscilaciones. El sistema resuena con la fuerza externa; vibra con mucha más intensidad que si la fuerza tuviera otra frecuencia diferente.
Tenemos que provocar esto en el simulador. Activemos la opción "Oscilador Forzado". Aparece un control para la frecuencia forzada, $$\omega_d$$, y una guía que nos indica las frecuencias de resonancia del sistema, sus frecuencias naturales $$\omega_n$$.
Ajustemos la frecuencia forzada para que coincida con una de ellas, por ejemplo, la del primer modo normal.
Vale. Un pequeño truco práctico: conviene añadir un poquito de amortiguamiento, B, un valor bajo como 0.05. ¿Por qué hacemos esto?
Porque en un sistema ideal sin amortiguamiento, en resonancia pura, la amplitud teóricamente crecería sin límite.
Uy. Lo cual no es muy realista ni manejable en la simulación. Un pequeño amortiguamiento representa las pérdidas de energía que siempre existen en sistemas reales y permite que la amplitud crezca mucho, pero se estabilice en un valor alto y constante. Esto nos deja observar el llamado estado estacionario de la resonancia.
Entendido. Entonces, con la frecuencia forzada ajustada a una de resonancia y un ligero amortiguamiento, damos a play. Puede que al principio el movimiento sea un poco irregular, eso se llama el transitorio, mientras el sistema se ajusta, pero al cabo de unos instantes...
Observa cómo el sistema entero se pone a oscilar con una amplitud enorme. Y no solo eso, fíjate en el patrón de movimiento de las masas.
Adopta exactamente la forma del modo normal cuya frecuencia hemos igualado. Es increíble.
Sí. Es como si el sistema estuviera "escuchando" la frecuencia de la fuerza externa y respondiera con entusiasmo solo cuando coincide con una de sus "notas" preferidas. Responde selectivamente.
Exacto, es una respuesta muy selectiva en frecuencia.

Conclusión y Próximos Pasos

Qué viaje acabamos de hacer. Empezamos con una sola masa oscilando y hemos llegado a descomponer movimientos complejos en modos normales, a construir ondas sumando esos modos, hemos distinguido tipos de ondas, creado batidos y hasta provocado una resonancia impresionante.
La verdad es que poder ver y manipular estos conceptos con el simulador los hace mucho más tangibles que, bueno, que en una pizarra.
Espero que quienes nos escuchan y quizá experimentan a la vez estén disfrutando tanto como nosotros.
Sin duda. La interactividad es clave aquí. Poder cambiar parámetros como la masa m, la rigidez del resorte k, el amortiguamiento B o el número de masas N, y ver de inmediato cómo afecta al movimiento, a las frecuencias, a la energía, es una forma de aprender muy poderosa. Se alinea muy bien con la filosofía de aprendizaje activo y visual de plataformas como Aula Quest.
Totalmente. Así que la invitación está abierta. Ahora que tenemos las bases, hay que seguir experimentando. Probar a cambiar los parámetros del sistema, ver qué pasa con los modos normales, jugar con distintas combinaciones en superposición, observar cómo un amortiguamiento mayor o menor afecta a la agudeza de la resonancia o la rapidez con que se disipa la energía inicial... Hay un montón de descubrimientos esperando en esos controles.
Y para dejar una idea flotando... bueno, hemos visto la conservación de energía y la disipación. Hemos visto cómo la onda viaja por la cadena en el modo "real". Pero, pensando un poco más allá, ¿cómo se transfiere exactamente la energía de una masa a la siguiente a través del resorte que las une? ¿El mecanismo es idéntico para una onda transversal (movimiento arriba-abajo) que para una longitudinal (movimiento izquierda-derecha)? Y, ¿la velocidad a la que viaja esa energía por la cadena dependerá de la rigidez k de los resortes o de la inercia m de las masas? Es algo en lo que pensar mientras se sigue explorando.
Excelente punto para reflexionar. Muchísimas gracias por acompañarnos en esta exploración tan visual. ¡Hasta la próxima!

Tu recurso completo para el Simulador de Oscilaciones Acopladas.

¿Cuál es el objetivo de este simulador de oscilaciones y cómo se usa?

Este laboratorio virtual de ondas y oscilaciones es una herramienta diseñada para entender los conceptos de modos normales, superposición, batidos, oscilaciones forzadas y resonancia de una manera visual e interactiva.

Controles Principales:

  • Número de Masas: Aumenta o disminuye la cantidad de osciladores en la cadena.
  • Parámetros del Sistema: Ajusta la masa ($m$), la constante elástica ($k$) y el amortiguamiento ($b$).
  • Modo de Simulación: Cambia entre el comportamiento 'Real', la visualización de 'Modos Normales' individuales, y la 'Superposición' de varios modos.
  • Oscilador Forzado: Activa una fuerza externa periódica para estudiar la resonancia.
  • Herramientas de Visualización: Activa las gráficas y la regla para un análisis detallado.

¿Por dónde empiezo? Un primer experimento sencillo.

Esta simulación es muy potente, ¡pero no te abrumes! El mejor punto de partida es el caso más simple: el oscilador armónico.

Pasos sugeridos:

1. Reduce el sistema: Usa el botón '-' para tener solo 1 Masa. Ahora tienes un Oscilador Armónico Simple (una masa unida a dos resortes).

2. Dale movimiento: En modo 'Real', arrastra la masa hacia un lado y suéltala. Observa su movimiento periódico y senoidal.

3. Analiza su frecuencia: Ve al modo 'Normal'. Verás que solo hay un modo de vibración, que es la frecuencia natural del sistema.

4. Comprueba la energía: Vuelve al modo 'Real', dale movimiento y activa la 'Gráfica Energía-Tiempo'. Con el amortiguamiento a cero, comprueba que la energía total (T) es una línea recta perfecta.

5. Añade complejidad: Ahora, aumenta a 2 Masas. Repite los pasos anteriores. ¿Qué ha cambiado? Verás que ahora hay dos modos normales y que el movimiento en 'Real' es más complejo. Has descubierto los fundamentos de las oscilaciones acopladas.

¿Qué es un Modo Normal y cómo los interpreta el simulador?

Un modo normal de vibración es un patrón de movimiento en el que todas las partes de un sistema oscilan a la misma frecuencia, llamada "frecuencia de modo normal". Un sistema con $N$ masas tiene $N$ modos normales distintos.

En este simulador, para un sistema uniforme (masas y resortes idénticos), estas frecuencias se calculan con la fórmula:

$$ \omega_n = 2\sqrt{\frac{k}{m}} \sin\left(\frac{n\pi}{2(N+1)}\right) \quad \text{para } n=1, 2, ..., N $$
Prueba en el simulador:

1. Selecciona el modo de simulación 'Normal'.

2. En el panel que aparece, puedes ver cada modo listado con su frecuencia teórica ($\omega_n$).

3. Haz clic en cada modo para ver cómo el sistema oscila en ese patrón específico. Observa que todas las masas se mueven sincrónicamente.

¿Qué diferencia hay entre ondas longitudinales y transversales?

Esta es una de las distinciones más importantes en el estudio de las ondas, y este simulador te permite verla claramente.

  • En una onda transversal, las partículas del medio oscilan en una dirección perpendicular a la dirección de propagación. Piensa en una cuerda de guitarra o en la superficie del agua: las partículas se mueven hacia arriba y hacia abajo, mientras la onda avanza hacia adelante.
  • En una onda longitudinal, las partículas oscilan en la misma dirección que la propagación. Un ejemplo típico es el sonido, que viaja como una serie de compresiones y expansiones del aire.
Prueba en el simulador:

1. Usa 4 o 5 masas en modo 'Real'.

2. Selecciona la opción 'Transversal' y mueve una masa de un extremo hacia arriba o abajo para crear un pulso. Observa cómo el "pico" de la onda viaja a lo largo de la cadena.

3. Cambia a 'Longitudinal' y mueve la misma masa hacia la izquierda o derecha. Verás cómo se genera una "compresión" que se desplaza a lo largo de la cadena.

4. ¿Qué tienen en común? Aunque visualmente son diferentes, ambos tipos de onda transmiten energía de un extremo a otro sin que las masas viajen con la onda (cada masa oscila alrededor de su posición de equilibrio). La estructura matemática es análoga: ambos muestran modos normales, resonancia y fenómenos como los batidos, aunque las frecuencias concretas dependen de la dirección y parámetros del sistema.

¿Qué diferencia hay entre el modo 'Real', 'Normal' y 'Superposición'?

El movimiento real de un sistema es siempre una combinación de sus modos normales. Estos modos te ayudan a entenderlo:

  • Modo Real: Simula la física completa, incluyendo colisiones y fuerzas. Si estiras una sola masa y la sueltas, el movimiento resultante es complejo porque has excitado una combinación de múltiples modos normales.
  • Modo Normal: Es una visualización idealizada. Te muestra cómo sería el movimiento si el sistema vibrara únicamente en uno de sus patrones puros. Es una herramienta de aprendizaje para aislar y entender cada componente del movimiento.
  • Modo Superposición: Te da el control para ser el "arquitecto" del movimiento. Puedes sumar manualmente los modos normales que quieras, ajustando sus amplitudes y fases para construir ondas complejas, como los batidos.

¿Qué son los Batidos (Beats) y cómo puedo verlos aquí?

Los batidos (o pulsaciones) son un fenómeno de interferencia que ocurre cuando se suman dos ondas de frecuencias muy parecidas ($\omega_1 \approx \omega_2$). El resultado es una onda cuya amplitud parece aumentar y disminuir periódicamente.

Prueba en el simulador:

1. Ve al modo 'Superposición'.

2. Pulsa el botón 'Generar Batidos'. El simulador activará automáticamente los dos modos normales con las frecuencias más cercanas.

3. Activa la 'Gráfica Posición-Tiempo' y dale a 'Play'. Verás claramente cómo la amplitud de la onda (la envolvente de la oscilación) sube y baja, creando el patrón de batido característico.

4. ¡Experimenta! Prueba a sumar manualmente otros pares de modos para ver si se producen batidos o patrones más complejos.

¿Qué representa la gráfica de Energía y por qué oscila tan rápido?

La gráfica de energía te permite analizar la conservación y transferencia de energía en el sistema. Muestra la Energía Cinética Total ($K$), la Energía Potencial Total ($P$) y la Energía Mecánica Total ($T = K + P$).

La energía oscila al doble de frecuencia que la posición. Esto es físicamente correcto, ya que la energía (que depende de $x^2$ y $v^2$) completa un ciclo de transformación (de potencial a cinética y de vuelta a potencial) dos veces por cada ciclo completo de oscilación de la masa.

Prueba en el simulador:

1. En modo 'Real', pon el 'Amortiguamiento' a cero y dale movimiento a una masa.

2. Activa la 'Gráfica Energía-Tiempo'. Verás cómo $K$ (naranja) y $P$ (azul) se intercambian, pero su suma, $T$ (blanca), permanece constante, demostrando la conservación de la energía.

3. Ahora, aumenta el amortiguamiento. Observa cómo la línea de energía total $T$ comienza a decaer, mostrando la disipación de energía.

¿Qué es la Resonancia y cómo la provoco en el simulador?

La resonancia es un fenómeno que ocurre cuando se aplica una fuerza externa periódica a un sistema oscilante a una frecuencia ($\omega_d$) que es igual o muy cercana a una de sus frecuencias naturales de vibración (sus frecuencias de modo normal, $\omega_n$). El resultado es una transferencia muy eficiente de energía que provoca un aumento drástico en la amplitud de la oscilación.

Prueba en el simulador de resonancia:

1. Activa el 'Oscilador Forzado'. Verás que aparece una guía con las "Frec. Resonancia".

2. Ajusta el deslizador de 'Frecuencia Forzada' para que coincida con uno de esos valores.

3. Añade un poco de 'Amortiguamiento' (ej. 0.05) para evitar que la amplitud crezca infinitamente y para observar el estado estacionario.

4. Dale a 'Play'. Tras un breve período 'transitorio' caótico, verás cómo el sistema se asienta en una oscilación de gran amplitud con el patrón del modo normal que has excitado.

Zona de Actividades de tu Profesor

Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.

¿Tu última clase con la simulación fue un éxito?

Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Crear una actividad es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.

  • 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
  • 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
  • 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
📤 Subir mi actividad

*Esto es solo para profes. Si lo eres, pide tu acceso.

Simulaciones en Física

No necesitas dar la clase perfecta

Solo necesitas que tus alumnos entiendan. Usa nuestras simulaciones y cambia el chip sin perder tiempo ni energía.

Zona Profe
Comparte con tus compañeros de clase