Simulador suma de vectores

📏 Laboratorio de Vectores: Suma, Escalares y Componentes

Domina las operaciones con vectores con este completo simulador interactivo 4 en 1. Nuestra herramienta online es un laboratorio de vectores que te permite trabajar en 1D, 2D y coordenadas polares. Realiza la suma de vectores de forma gráfica y experimenta con la multiplicación por un escalar.

Esta simulación de vectores va más allá de una simple suma. Úsala para:
  • Visualizar sus componentes: Descompón cualquier vector en sus partes rectangulares (x, y) o como una proyección sobre los ejes.
  • Entender los métodos gráficos: Observa cómo se construye el vector resultante con la regla del paralelogramo o del polígono.
  • Dominar la multiplicación escalar: Multiplica un vector por un número y comprueba al instante cómo afecta a su módulo y sentido.
Categoría Mate > Geometría
Nivel educativo ESO
Dificultad Media (4/10)
Visitas 40

📋 Detalles de la simulación

¿Qué te ha parecido la simulación?

★★★★★
5,0 de 5 (3 valoraciones)

Explorando el Laboratorio de Vectores: Suma, Escalares y Componentes

Hola a todos los estudiantes de Aula Quest. Bienvenidos. Hoy vamos a hacer una exploración, ¿eh?, bastante a fondo del mundo de los vectores.
Vamos a usar como guía un material que describe un laboratorio de vectores, que habla de suma, escalares, componentes. La idea es entenderlos, pero sobre todo ver cómo funcionan de forma interactiva.
Perfecto. Queremos desgranar las operaciones clave: cómo se suman, qué pasa si los multiplicamos por un número (un escalar que llaman) y qué son las componentes.
Y lo haremos imaginando que tenemos delante esa simulación que describe el material. Que, por cierto, parece una herramienta muy completa, ¿no?
Como un cuatro en uno. Cubre 1D, 2D, coordenadas polares y hasta un laboratorio general para experimentar más libremente. Promete ser muy visual, muy práctico. Bueno, pues vamos a ello.
Vamos. Totalmente. Y, antes de meternos de lleno, eh, conviene recordar por qué son tan importantes los vectores. Son, básicamente, el lenguaje que usamos en física, en ingeniería, bueno, en muchas ciencias.
Para describir cualquier cosa que tenga magnitud y dirección: fuerza, velocidad... Y sí, una simulación como la que se describe es, la verdad, una forma genial de pillar estos conceptos.
Te permite ver cosas que, en papel, a veces cuestan un poco más. Es como tocar las mates, casi.
Eso de "tocar las mates" me gusta. A ver, empecemos por lo básico: la suma. Queremos encontrar el vector resultante, el que tiene el mismo efecto que los originales juntos.
El material dice que hay dos formas gráficas principales de verlo: el método del polígono y el del paralelogramo. Aquí la simulación seguro que ayuda mucho.
Correcto. El del polígono, tal como lo pintan para 1D y 2D, parece súper intuitivo. El proceso suena muy directo y, la verdad, bastante ameno. Te dicen que hay un menú con vectores base, ¿no? Los llaman $A$ y $B$.
Y lo interesante es cómo interactúas. Los coges... del menú. Literalmente los arrastras.
Eso parece indicar. Los seleccionas del menú y los arrastras al espacio de trabajo, como si fueran piezas, bloques de construcción que puedes mover.
Ah, vale. Eso sí que suena didáctico.
Y divertido, como decías.
Justo. La descripción da a entender que la simulación es inteligente. Al soltar el segundo vector, digamos $B$, lo coloca justo al final del primero, $A$. Punta con origen, ¿sabes?
Y entonces, ¡pam!, aparece el vector suma, lo llaman $S$. Y va desde el origen del primero hasta el final del último. Este sistema de arrastrar y soltar...
Hace que la regla se vea clarísima, sin tener que pensarla mucho.
Exacto. Ves la cadena de vectores y el resultado final. Muy visual, sí.
Entendido. Una forma muy gráfica. Y luego está el otro, el del paralelogramo. El texto dice que es útil sobre todo para sumar dos vectores. ¿Cómo se vería este?
Bueno, aquí la geometría nos da otra visión, pero llega al mismo sitio. Según cuentan, en la simulación 2D, hay una opción para verlo así. Quizás en un menú llamado "Componentes" o algo parecido.
Seleccionas "paralelogramo" o como se llame la opción, y entonces la simulación dibuja los dos vectores, $A$ y $B$, saliendo del mismo punto.
Ah, vale. No uno detrás del otro, sino desde el mismo origen.
Eso es. Y luego traza las líneas paralelas para completar el paralelogramo. Y la clave está en la diagonal, la que sale del origen común.
Esa diagonal es, precisamente, el vector suma $S$, el mismo de antes. Es elegante, ¿no?, ver cómo la geometría te da la respuesta.
Sí, la verdad. Dos formas de ver lo mismo. Vale, métodos gráficos de suma claros. Pasemos a otra cosa: coordenadas polares. A veces imponen un poco más que las cartesianas ($x, y$) de toda la vida.
El material usa una analogía que está bien. Las cartesianas son como dar direcciones en una cuadrícula: "tres al este, dos al norte". Las polares, en cambio, te dan la longitud total (magnitud $r$) y la dirección (el ángulo $\theta$).
Sería más como decir "camina 5 metros justo... allí", señalando.
Es más directo para magnitud y orientación, sí. Y la simulación específica para polares parece diseñada justo para eso. La descripción sugiere que hay controles, quizás deslizadores, para ajustar $r$ y $\theta$ directamente.
Pones los valores, pulsas "añadir vector" y listo. Y parece que puedes añadir varios así y te muestra la suma resultante, también en polares si quieres.
Pero mencionan un "truco útil". ¿A qué se refieren? ¿Hay alguna forma de simplificarlo?
Ah, sí. Eso es interesante. Es la conexión entre los dos sistemas. A ver, definir vectores en polares ($r, \theta$) es conceptualmente claro, pero sumarlos directamente así, mmm, matemáticamente se puede complicar.
El "truco", o la función útil que describen, es activar una opción, algo como "mostrar valores cartesianos". ¿Y qué hace eso?
Pues que la simulación te calcula las componentes $x$ e $y$ de cada vector polar que has creado. Y aquí viene lo bueno: sumar vectores es muchísimo más fácil si sumas las $x$ por un lado y las $y$ por otro.
Que es algo que veremos ahora con más detalle, lo de las componentes. Pero esto ya nos dice algo importante: a veces, cambiar de sistema de coordenadas es la clave para resolver algo. Usamos las cartesianas para facilitar una operación que estábamos pensando en polares.
Entendido, entendido. O sea, las polares para definirlo intuitivamente, pero las cartesianas para operar más fácil. Tiene lógica. Venga, siguiente operación: multiplicación por un escalar.
Recordamos: un escalar es solo un número, sin dirección. ¿Qué le hace a un vector? La idea clave que resalta el texto es que cambia el tamaño (la magnitud) y puede cambiar el sentido (si apunta para un lado o el contrario).
Pero lo que no cambia nunca es la dirección sobre la que actúa, la línea. Usan palabras como "amplificar" o "reducir" el vector.
Exacto. Las reglas son muy lógicas, la verdad. Si multiplicas por un escalar mayor que 1, pongamos 3, pues el vector se hace tres veces más largo, se amplifica.
Si el escalar está entre 0 y 1, como 0.5, pues se acorta, se reduce a la mitad. Y si es negativo, por ejemplo -2, pasan dos cosas: una, invierte el sentido, gira 180 grados, apunta al revés.
Y dos, su longitud se multiplica por el valor absoluto, o sea, por 2 en este caso. Se haría el doble de largo y apuntaría al revés.
Vale, reglas claras. ¿Y cómo se juega con esto en el "laboratorio general" que mencionan? ¿Cómo se ve el cambio?
El laboratorio general parece el modo más libre. La descripción dice que primero defines un vector $A$ como tú quieras, y luego, en una sección de "Operación", en vez de sumar otro vector, metes un número, el escalar.
Y lo interesante es que, según dicen, el efecto es instantáneo. El vector resultante ($R$ lo llaman) cambia de tamaño o sentido en la pantalla al momento. Ves el efecto directo del escalar.
Una respuesta visual inmediata. Eso ayuda a entenderlo.
Y entender esto es básico, porque, como apunta la fuente, está detrás de muchas leyes físicas. El ejemplo típico, la segunda ley de Newton: $$ \vec{F} = m \cdot \vec{a} $$ Fuerza ($\vec{F}$) y aceleración ($\vec{a}$) son vectores; masa ($m$) es un escalar positivo. Aquí se ve perfecto: la fuerza y la aceleración que produce siempre van en la misma dirección.
La masa, el escalar, solo dice cuánta fuerza para una aceleración, o viceversa, pero no desvía la aceleración respecto a la fuerza.
Buena conexión. Sí. Va más allá de la fórmula. Y nos queda el último punto importante: las componentes de un vector.
El material las llama "sombras" o "proyecciones" sobre los ejes $x$ e $y$. E insisten mucho en que descomponer en componentes simplifica las operaciones. ¿Por qué son tan útiles?
¡Uf! Son cruciales, absolutamente. Piensa en sumar varios vectores inclinados usando solo la regla del polígono. Si son muchos, puede ser un lío gráfico o trigonométrico tremendo.
Pero si cada vector lo partes en su trozo horizontal (componente $x$) y su trozo vertical (componente $y$), el problema cambia por completo.
¿Cómo cambia? ¿Qué es lo que se simplifica tanto?
La suma en sí. A ver, todas las componentes $x$ van en la misma línea, el eje horizontal. Positivas o negativas, pero en esa línea. Y todas las $y$ igual, en el eje vertical.
Así que, para hallar la $x$ total del resultado, ya no haces geometría rara, solo sumas y restas números. Todas las $x$ juntas y lo mismo para la $y$ total. Has cambiado sumar flechas inclinadas por sumar números en dos direcciones perpendiculares.
Ah, claro. Conviertes un problema geométrico en dos problemas aritméticos sencillos.
¡Exactamente! Y además te permite analizar cosas complejas tratando por separado lo que pasa en horizontal y en vertical, como el movimiento de un proyectil, por ejemplo.
Vale. Ahora veo por qué es tan fundamental. De geometría vectorial a aritmética de componentes. ¿Y cómo se visualiza esto en las simulaciones? ¿Se ven esas "sombras"?
Pues, según el material, sí. Tanto en el laboratorio general como en la simulación 2D. Debe haber opciones en algún menú, quizás "Componentes" o "Vistas", para activar la visualización rectangular o "proyección en ejes".
Al hacerlo, la simulación te dibuja esas sombras sobre los ejes $x$ e $y$. Y lo potente, según describen, es que si mueves el vector principal, cambias su longitud o su ángulo, ves en tiempo real cómo cambian sus componentes, cómo crecen o decrecen.
Eso da una comprensión muy dinámica de cómo se reparte la influencia del vector en cada eje.
Claro. Y si lo pensamos un poco más allá, la descomposición vectorial no es solo un truco de cálculo, es una de las herramientas de análisis más potentes que hay. En física, ingeniería, hasta en economía o gráficos por ordenador.
Permite coger problemas complejos y partirlos en cachitos más manejables que actúan en direcciones perpendiculares. Simplifica muchísimo el análisis.
La verdad es que ha sido una exploración muy completa. Hemos visto las funciones clave de este laboratorio virtual y cómo ayuda a visualizar y, bueno, a entender mejor estas operaciones.
Si hacemos un repaso rápido, vimos cómo la simulación permite jugar a sumar vectores con el polígono y el paralelogramo, y esa interacción de arrastrar y soltar que parece tan didáctica.
Pasamos por las coordenadas polares ($r, \theta$) y vimos esa conexión útil con las cartesianas ($x, y$) para simplificar las sumas. Entendimos bien cómo un escalar estira, encoge o invierte un vector con esa respuesta visual inmediata en el laboratorio y la conexión con $F=ma$.
Y finalmente, la importancia de las componentes $x$ e $y$, no solo para calcular, sino como herramienta de análisis potente. Queda claro que estas herramientas visuales e interactivas son una ayuda enorme para aprender.
Entonces, la conclusión principal sería que dominar estas operaciones es esencial, y visualizarlas así lo hace mucho más fácil, ¿no?
Exacto. Y como reflexión final, sobre todo para los estudiantes de Aula Quest que estáis con esto ahora. Hemos visto las operaciones básicas, pero lo fascinante es pensar cómo estos mismos principios —sumar, multiplicar por escalar, descomponer— son la base para modelar cosas increíblemente complejas.
Se usan para predecir el tiempo, las corrientes marinas, para calcular órbitas de satélites, diseñar puentes, hasta para animar personajes en videojuegos. La pregunta para darle una vuelta es: más allá de la física y las mates obvias, ¿dónde más podrían estar funcionando estas reglas vectoriales sin que nos demos cuenta, en nuestro día a día, en tecnologías que usamos?
Quizás si miramos el mundo con "ojos vectoriales", empezamos a ver estas estructuras en sitios inesperados.

¿Qué es este Laboratorio de Vectores?

Este Laboratorio de Vectores es un simulador interactivo 4 en 1 diseñado para que domines las operaciones vectoriales. Te permite trabajar en 1D, 2D y coordenadas polares para que puedas:

  • Realizar la suma de vectores de forma gráfica.
  • Experimentar con la multiplicación por un escalar.
  • Descomponer vectores en sus componentes.
  • Convertir coordenadas polares a cartesianas y viceversa.

¿Cómo se suman vectores gráficamente?

La suma de vectores consiste en encontrar un único vector resultante que produce el mismo efecto que los vectores originales juntos. Los dos métodos gráficos más comunes son:

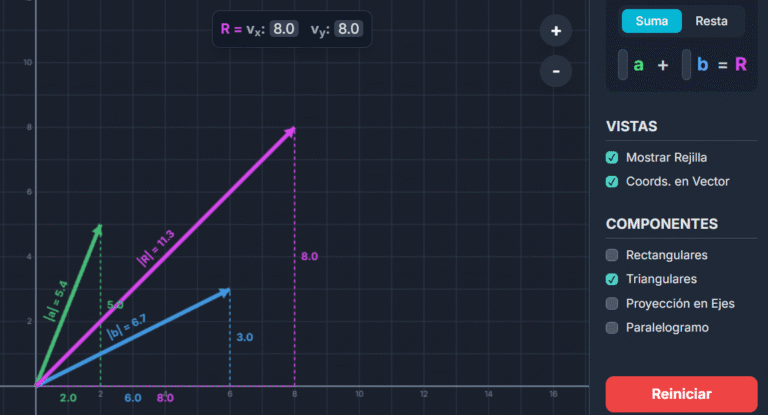
  • Método del Polígono: Se coloca un vector a continuación del otro. El resultante va desde el origen del primero hasta el extremo del último.
  • Método del Paralelogramo: Se unen los orígenes de dos vectores y se forma un paralelogramo. El resultante es la diagonal que parte del origen común.
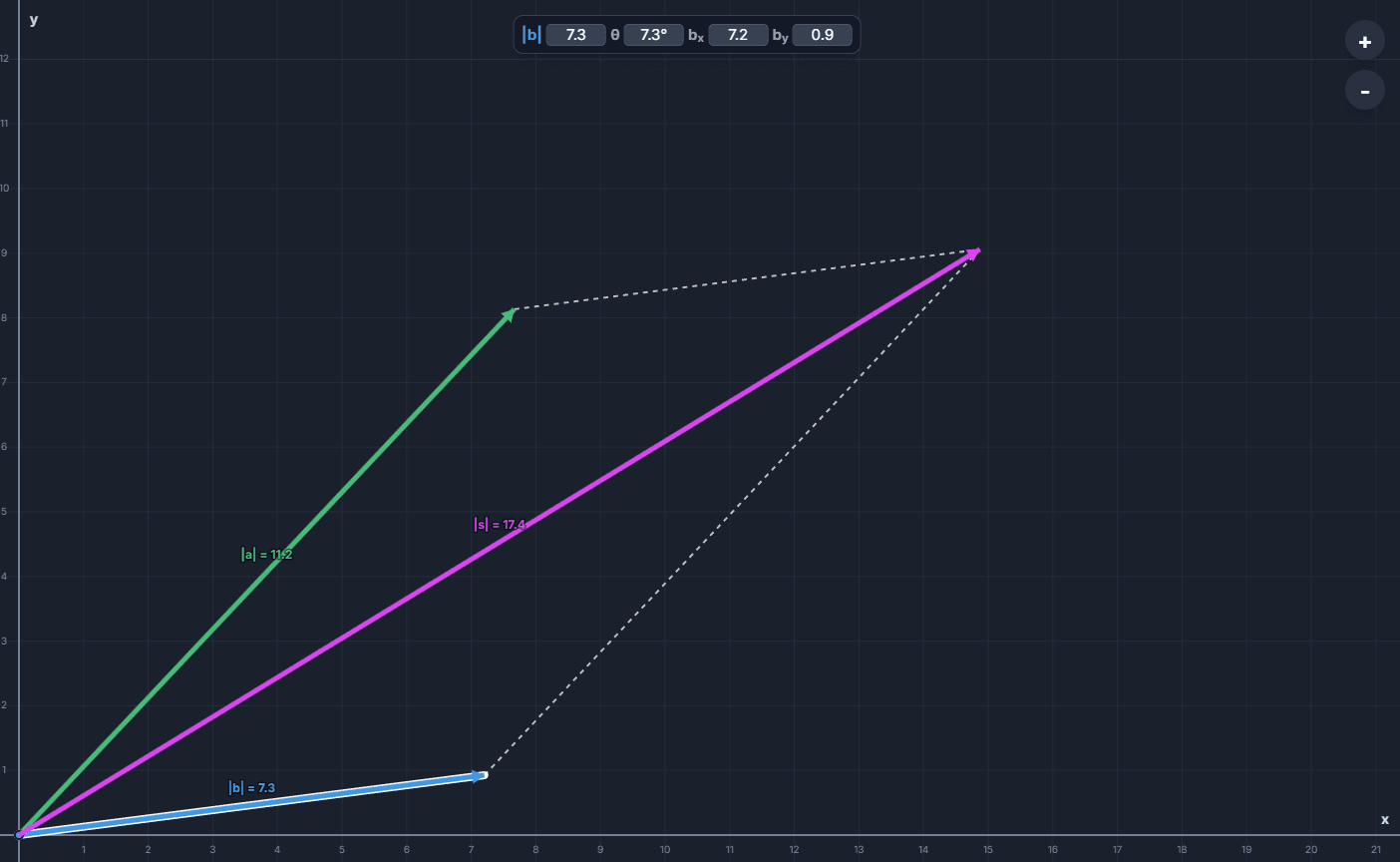
Método del paralelogramo para sumar vectores.
El método del paralelogramo es ideal para visualizar la suma de dos vectores.

Prueba esto en el simulador 2D: Arrastra los vectores 'a' y 'b'. Verás que se aplica el método del polígono. Ahora, activa la opción Paralelogramo en el menú "COMPONENTES" para ver cómo se forma la figura y la diagonal resultante.

¿Cómo se convierte un vector de polares a cartesianas?

Convertir un vector de coordenadas polares (magnitud r, ángulo θ) a cartesianas (x, y) es fundamental en física. Se usan las siguientes fórmulas trigonométricas:

x = r ⋅ cos(θ)

y = r ⋅ sin(θ)

Ejemplo práctico: Imagina un vector con magnitud r = 10 y ángulo θ = 30°.

  • Componente x = 10 ⋅ cos(30°) = 10 ⋅ 0.866 = 8.66
  • Componente y = 10 ⋅ sin(30°) = 10 ⋅ 0.5 = 5.0

Compruébalo en la simulación de Vectores en Polares: Crea un vector con r=10 y θ=30°. Luego, en el menú "VISTAS", activa Mostrar Valores Cartesianos. Verás que las componentes (x, y) coinciden con nuestro cálculo.

¿Qué es la multiplicación por un escalar?

La multiplicación de un vector por un escalar (un simple número) es una operación que cambia el tamaño y/o el sentido del vector, pero nunca su dirección. Es como "amplificar" o "reducir" el vector.

  • Si multiplicas por un número > 1, el vector se alarga.
  • Si multiplicas por un número entre 0 y 1, se acorta.
  • Si multiplicas por un número negativo, cambia de sentido (apunta al lado contrario).

Abre el Laboratorio General para experimentar: Define un vector 'a'. Luego, en la sección "OPERACIÓN", introduce un número en la casilla del escalar. Observa cómo el vector resultante 'R' cambia de tamaño y sentido al instante. Este es el fundamento de conceptos como la segunda ley de Newton (F = m·a).

¿Y cómo se restan los vectores?

La resta de vectores, como a - b, es en realidad un caso especial de la suma. Equivale a sumar al vector 'a' el opuesto del vector 'b', es decir: a + (-b).

El vector opuesto (-b) es un vector que tiene la misma magnitud y dirección que 'b', pero su sentido es exactamente el contrario (apunta 180° en la otra dirección).

Experimenta en el Laboratorio General: Define dos vectores, 'a' y 'b'. Primero, selecciona la operación de Suma para ver el resultado. Luego, cambia a Resta. El simulador te mostrará gráficamente el vector -b y calculará el nuevo resultante. ¡Es la forma más clara de ver la diferencia!

¿Para qué sirven las componentes de un vector?

Las componentes de un vector son sus proyecciones sobre los ejes de coordenadas (normalmente X e Y). Descomponer un vector es una técnica clave porque simplifica operaciones complejas.

Sumar vectores inclinados puede ser difícil, pero sumar sus componentes es tan fácil como sumar números normales: se suman todas las componentes 'x' por un lado y todas las 'y' por otro.

Explora esto en el Laboratorio General o en la simulación 2D: En el menú "COMPONENTES", activa la vista Rectangulares o Proyección en Ejes. Mueve el vector principal y observa cómo sus componentes cambian de tamaño. Esta es la base del análisis vectorial en física e ingeniería.

¿Qué es el método analítico para sumar vectores?

El método analítico es la forma más potente y precisa de sumar vectores, y se basa en sus componentes. El proceso es muy simple:

  1. Descomponer: Encuentra las componentes (x, y) de cada vector que quieres sumar.
  2. Sumar: Suma todas las componentes 'x' por un lado y todas las componentes 'y' por otro.
  3. Recomponer: Con las componentes resultantes (Rx, Ry), puedes encontrar la magnitud y el ángulo del vector resultante final si lo necesitas.

Este método elimina los errores de los dibujos a escala y funciona para sumar cualquier cantidad de vectores. Es el poder de las componentes en acción, algo que puedes verificar fácilmente en nuestro laboratorio de vectores interactivo.

¿Por qué es importante saber todo esto?

Los vectores no son solo flechas en un papel; son el lenguaje de la física y la ingeniería. Aprender a operar con ellos es fundamental para describir el mundo real.

  • Fuerzas: Para saber hacia dónde se moverá un objeto cuando varias fuerzas actúan sobre él (como la gravedad, una tensión y un empuje).
  • Velocidades: Para calcular la velocidad real de un avión afectado por el viento o de un barco en una corriente.
  • Campos: Para entender cómo funcionan los campos eléctricos y magnéticos.

Dominar la suma, resta y descomposición de vectores te da la base para resolver problemas complejos del mundo real. ¡Y este simulador es tu campo de entrenamiento perfecto!

Zona de Actividades de tu Profesor

Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.

¿Tu última clase con la simulación fue un éxito?

Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Crear una actividad es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.

  • 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
  • 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
  • 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
📤 Subir mi actividad

*Esto es solo para profes. Si lo eres, pide tu acceso.

Otras Simulaciones en Mate

No necesitas dar la clase perfecta

Solo necesitas que tus alumnos entiendan. Usa nuestras simulaciones y cambia el chip sin perder tiempo ni energía.

Zona Profe
Comparte con tus compañeros de clase