Simulador de Sistemas de Ecuaciones 2x2

🧮 Domina los sistemas 2×2 con claridad (y sin fórmulas de más)

Resolver sistemas de ecuaciones ya no será un dolor de cabeza. Con este simulador puedes probar los tres métodos clásicos —sustitución, igualación y reducción— y ver cómo se representan gráficamente las rectas hasta encontrar el punto donde se cruzan.
Ideal para repasar antes de un examen, reforzar lo aprendido en clase o simplemente quitarte el miedo a las ecuaciones con dos incógnitas.

📋 Detalles de la simulación

  • 📂 Categoría: Álgebra
  • 🎓 Nivel educativo: ESO
  • ⚙️ Dificultad: Media
  • 📈 N.º de veces usada: 46
Ver en pantalla completa

Sistemas de Ecuaciones 2x2: Guía Completa de Métodos de Solución

Hola estudiantes de Aula Quest. Hoy vamos a meternos a fondo con algo súper útil: los sistemas de ecuaciones lineales 2x2.
Eso es. Vamos a ver los cuatro métodos clásicos: Sustitución, Igualación, Reducción y el Gráfico.
La idea no es solo aprender los pasos, sino pillar por qué funciona cada uno, ¿verdad?
Exacto. A ver, un sistema 2x2, para que todo el mundo lo tenga claro, son dos ecuaciones. Lineales, importante, o sea, con $x$ e $y$ sin exponentes raros, elevados a 1. Y dos incógnitas, claro, la $x$ y la $y$.
Vale. Y lo que buscamos es el par de números, un valor para $x$ y otro para $y$, que hagan que las dos ecuaciones sean verdad, a la vez.
Perfecto. Pues para que sea más fácil seguirlo, vamos a usar un sistema de ejemplo todo el rato. ¿Qué tal? $$ x + y = 4 $$ Y la segunda: $$ x - y = 2 $$
Ya, bueno, haciendo una comprobación rápida sabemos que la solución va a ser $x=3$ e $y=1$.
Efectivamente, porque $3+1=4$ y $3-1=2$. Funcionan las dos.
Genial. Pues vamos a ver cómo llegamos a ese $x=3$ e $y=1$ con el primer método. Empezamos por Sustitución.
Venga. Pues, eh, la sustitución, como dice el nombre, va de sustituir. Coges una ecuación, la que te parezca más fácil, y despejas una de las incógnitas.
A ver, en $x+y=4$ podríamos despejar la $x$, por ejemplo.
Sí, y quedaría $x=4-y$. Fácil, ¿no?
Sí, sencillo.
Vale, pues ahora esta expresión, $4-y$, que es igual a $x$, la metemos en la otra ecuación. En la de $x-y=2$.
Justo. Donde pone $x$, ponemos $4-y$. Así que tenemos: $4-y-y=2$.
¡Ah! Y ahora solo hay $y$. Ya está casi.
Eso es. Operamos: $4-y-y$, pues $4-2y=2$.
Vale. Ahora, números a un lado, incógnitas al otro. El 4 pasa restando: $-2y = 2-4$, que es $-2$.
$-2y = -2$. Dividimos por $-2$ y, ¡tachán!, $y=1$.
Ya tenemos la $y$. Y para la $x$, volvemos a donde la despejamos. $x = 4-y$. Como $y=1$, pues $x=4-1$. $x=3$. Lo tenemos. $x=3$, $y=1$, primer método listo.
Exacto. Vale, pues ahora, Igualación. Con el mismo sistema: $x+y=4$, $x-y=2$. ¿Cómo va este?
Pues este tiene una simetría bonita. Aquí despejamos la misma incógnita en las dos ecuaciones.
Ah, vale. En la primera ya teníamos $x=4-y$.
Sí. Y en la segunda, $x-y=2$, si despejamos la $x$, pasamos la $y$ sumando: $x=2+y$.
Entendido. $x=4-y$ y también $x=2+y$.
Y ahora viene la igualación. Si $x$ es igual a una cosa y también es igual a otra, pues esas dos cosas tienen que ser iguales entre sí.
Claro, tiene sentido.
Entonces, $4-y$ es igual a $2+y$.
Exacto. Y otra vez, una ecuación con solo $y$. Agrupamos, pasamos la $y$ de la izquierda sumando a la derecha, y el 2 de la derecha restando a la izquierda.
Quedaría $4-2 = y+y$. O sea, $2 = 2y$.
Dividimos entre 2, y es $y=1$ otra vez.
Como debe ser. Y la $x$, igual que antes. Sustituyendo en $x=4-y$, nos da $x=3$. Mismo resultado, otro camino.
Muy bien, me va quedando claro. Ahora, el que a veces parece un poco más... mmm, no sé, ¿abstracto? La Reducción.
Sí, a veces parece magia, pero es pura lógica. La idea aquí es preparar las ecuaciones, si hace falta multiplicándolas por algún número, para que al sumarlas o restarlas, una de las incógnitas desaparezca.
Y en nuestro $x+y=4$, $x-y=2$, ¿hay que multiplicar?
Pues mira qué bien, en este caso concreto no hace falta. Fíjate en la $y$. En la primera ecuación está como $+y$ (coeficiente $+1$) y en la segunda como $-y$ (coeficiente $-1$).
¡Ostras, es verdad! Son opuestos.
Exacto. Así que si sumamos las dos ecuaciones, tal cual están, miembro a miembro...
A ver... $x+x + y+(-y)$, eso es $y-y$, igual a $4+2$.
Perfecto. $x+x$ es $2x$. $y-y$ es 0. Y $4+2$ es 6. Nos queda $2x=6$.
Directo. Dividimos entre 2 y $x=3$. ¡Rapidísimo!
¡Wow! Sí que ha sido rápido.
Y ahora, con $x=3$, vamos a la primera ecuación, por ejemplo. $3+y=4$. Pues $y=4-3$. $y=1$.
Impresionante. Para este sistema, la reducción ha sido la más directa.
Sí, cuando los coeficientes ya están así preparados, es muy eficiente.
Vale. Y nos queda el último método: el Gráfico. Aquí entra el plano cartesiano, ¿no?
Efectivamente. Cada ecuación lineal de dos incógnitas representa una recta en el plano. La solución del sistema es simplemente el punto donde esas dos rectas se cortan.
Entiendo. Para dibujarlas, lo mejor es ponerlas en la forma $y = mx+n$, ¿verdad? La forma explícita.
Eso es, despejar la $y$. En $x+y=4$, si despejamos la $y$, queda $y=-x+4$.
Vale, esa es una recta.
Y en la otra, $x-y=2$, despejamos: $-y = 2-x$. Cambiamos los signos a todo para tener la $y$ positiva. $y = -2+x$, o sea, $y=x-2$.
Exacto. Tenemos las dos rectas: $y=-x+4$ e $y=x-2$. Si ahora se dibujan estas dos rectas...
El punto donde se crucen será la solución, $(3,1)$.
Justo. Y esto la gente de Aula Quest lo puede ver muy bien en la simulación que tienen al lado. Meten las ecuaciones y ven el punto de corte.
Genial. Pero ojo, esto nos lleva a pensar, ¿siempre se cortan las rectas en un único punto?
Mmm, buena pregunta. Supongo que no. ¿Qué pasa si son paralelas?
Exacto. Si al despejar la $y$ nos encontramos con dos rectas que tienen la misma pendiente (el número que multiplica a la $x$, la $m$) pero distinta ordenada en el origen (el número suelto, la $n$), son paralelas.
Como $y=2x+3$ e $y=2x+5$. Misma inclinación, pero una empieza más arriba que la otra.
Eso es. Nunca se cortan. El sistema no tiene solución. Se dice que es incompatible.
Vale, paralelas, sin solución. ¿Y hay otra posibilidad?
Sí, que al despejar la $y$, nos quede exactamente la misma ecuación en ambos casos.
¿Cómo? Por ejemplo...
Imagina que una ecuación es $y=-x+4$ y la otra, tras simplificarla, también es $y=-x+4$. O que da $2y=-2x+8$, que es la misma.
Ah, vale. Es la misma recta dibujada una encima de la otra.
Exacto. Son rectas coincidentes. Todos sus puntos son comunes. El sistema tiene infinitas soluciones. Se llama compatible indeterminado.
Entendido. O se cortan en un punto (solución única), o son paralelas (sin solución), o son la misma recta (infinitas soluciones).
Esas son las tres posibilidades.
Bueno, pues hemos visto cuatro maneras de atacar el mismo problema: sustitución, igualación, reducción y el método gráfico. Cada uno con su enfoque.
Lo importante, de verdad, es entender el porqué de cada paso. ¿Por qué igualamos? ¿Por qué funciona la reducción? Más que memorizar, es pillar la lógica. Y animo a la gente a que juegue con la simulación, que pruebe otros sistemas, que compruebe.
Una pequeña reflexión. Hemos visto que para nuestro sistema $x+y=4$, $x-y=2$, la reducción fue súper rápida. ¿Qué pistas nos pueden dar las ecuaciones solo mirándolas para intuir qué método puede ser el más eficiente? ¿Cómo elegir la mejor estrategia sin empezar a calcular a lo loco? Ahí lo dejo.

🧩 Sistemas de ecuaciones 2×2

Un sistema de ecuaciones lineales con dos incógnitas es un conjunto de dos ecuaciones donde las variables (normalmente llamadas $x$ e $y$) están elevadas solo a la potencia 1, es decir, son lineales.

$$ \begin{cases} a \cdot x + b \cdot y = c \\ d \cdot x + e \cdot y = f \end{cases} $$

Los coeficientes $a$, $b$, $c$, $d$, $e$ y $f$ pueden ser enteros, decimales o fracciones. Nuestro objetivo es encontrar los valores de $x$ e $y$ que hacen que ambas ecuaciones se cumplan a la vez.

✅ ¿Qué significa resolver un sistema?

Resolver un sistema es encontrar los valores que cumplen simultáneamente las dos ecuaciones. No basta con que una pareja funcione en una sola ecuación: tiene que funcionar en las dos.

Por ejemplo, el sistema siguiente:

$$ \begin{cases} x + y = 4 \\ x - y = 2 \end{cases} $$

tiene solución $x = 3$, $y = 1$, porque al sustituir en ambas ecuaciones se cumple.

➡️ Puedes introducir este sistema en el simulador para comprobarlo. Luego, cambia los coeficientes y observa cómo cambia el resultado.

🔄 Método de sustitución

Este método se basa en despejar una variable en una de las ecuaciones y sustituir esa expresión en la otra ecuación.

Ejemplo:

$$ \begin{cases} x = 4 - y \\ 2x + y = 7 \end{cases} $$

Sustituimos $x = 4 - y$ en la segunda ecuación:

$$ 2(4 - y) + y = 7 $$

Resolvemos paso a paso:

  • $2 \cdot 4 = 8$
  • $2 \cdot (-y) = -2y$
  • $8 - 2y + y = 7$
  • $8 - y = 7$
  • $-y = -1 \Rightarrow y = 1$

Ahora sustituimos $y = 1$ en $x = 4 - y$:

$x = 4 - 1 = 3$

Solución: $x = 3$, $y = 1$

➡️ Usa el modo de sustitución en el simulador. Introduce las ecuaciones y verifica si los pasos coinciden con los tuyos.

⚖️ Método de igualación

En este método, despejamos la misma variable en ambas ecuaciones y después igualamos las expresiones obtenidas.

Ejemplo:

$$ \begin{cases} x = 2y + 1 \\ x = -y + 4 \end{cases} $$

Como ambas expresiones son iguales a $x$, las igualamos entre sí:

$$ 2y + 1 = -y + 4 $$

Resolviendo paso a paso:

  • $2y + y = 3y$
  • $4 - 1 = 3$
  • $3y = 3 \Rightarrow y = 1$

Ahora sustituimos en una de las ecuaciones:

$x = 2(1) + 1 = 3$

Solución: $x = 3$, $y = 1$

➡️ Prueba este sistema en el simulador con el método de igualación. Luego, cambia los coeficientes y vuelve a intentarlo.

🔁 Método de reducción

Este método consiste en eliminar una de las variables combinando las dos ecuaciones. Pero antes hay que prepararlas multiplicando por los coeficientes adecuados. Importante: si multiplicas una ecuación, lo haces en ambos miembros.

Ejemplo:

$$ \begin{cases} 3x + 2y = 16 \\ 2x - y = 1 \end{cases} $$

Queremos eliminar la $x$, así que multiplicamos para igualar sus coeficientes:

$$ \begin{cases} (3x + 2y) \cdot 2 = 6x + 4y = 32 \\ (2x - y) \cdot 3 = 6x - 3y = 3 \end{cases} $$

Ahora restamos las ecuaciones:

$$ (6x + 4y) - (6x - 3y) = 7y = 29 $$

Resolvemos:

$$ y = \frac{29}{7} $$

Y sustituimos en una ecuación original:

$$ 2x - \frac{29}{7} = 1 \Rightarrow x = \frac{18}{7} $$

Solución: $x = \frac{18}{7}$, $y = \frac{29}{7}$

➡️ Introdúcelo en el simulador, elige el método de reducción y comprueba los pasos. ¿Coinciden con los tuyos?

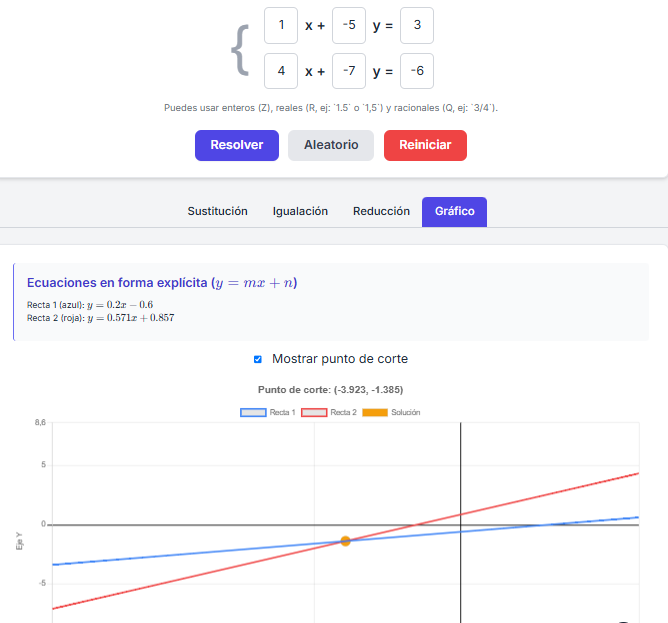
📈 Método gráfico

Para resolver gráficamente, transformamos cada ecuación a la forma explícita $y = mx + n$, donde:

  • $m$ es la pendiente: indica cuánto sube o baja la recta por cada paso en $x$.
  • $n$ es la ordenada en el origen: es decir, el punto donde la recta corta el eje $y$.

Ejemplo:

$$ \begin{cases} 2x + y = 4 \\ x - y = 1 \end{cases} $$

Despejamos $y$ en ambas ecuaciones:

  • Primera: $y = -2x + 4$
  • Segunda: $y = x - 1$

Ahora podemos dibujar ambas rectas en el plano y buscar su punto de corte. Ese punto es la solución del sistema.

➡️ Usa el modo gráfico del simulador. Introduce las dos ecuaciones y observa el cruce de las rectas. ¿Qué pasa si modificas un coeficiente?

🔍 Casos especiales

1. Rectas paralelas → Sistema incompatible

Si las rectas nunca se cruzan, es que el sistema no tiene solución. Son rectas con la misma pendiente pero distinta ordenada en el origen.

Ejemplo: $y = 2x + 1$ y $y = 2x - 3$

➡️ Pruébalo en el simulador. ¿Qué ves en la gráfica?

2. Rectas coincidentes → Sistema compatible indeterminado

Si las rectas se superponen por completo, es porque representan la misma ecuación. Entonces hay infinitas soluciones: todos los puntos de la recta valen.

Ejemplo: $2x + y = 4$ y $4x + 2y = 8$ (la segunda es el doble de la primera)

➡️ Introdúcelo en el simulador gráfico. ¿Se superponen las rectas?

🧠 Conclusión

El método de reducción te obliga a pensar con estrategia y operar con precisión. El gráfico te da una visión visual clara del sistema. Y el simulador te permite experimentar, corregir y aprender con libertad.

Ahora ya sabes identificar no solo la solución de un sistema, sino también cuándo no tiene solución o tiene infinitas. ¡Ese ojo matemático lo vas entrenando cada vez más!

🎯 ¿Listo para cazar soluciones con precisión matemática? Elige tu Misión

Ya has probado cómo se comporta un sistema 2×2 cuando cambias los coeficientes, has visto cómo se cruzan (o no) las rectas en el gráfico, y has experimentado con los distintos métodos: sustitución, igualación, reducción... y de manera gráfica.

Ahora es el momento de aplicar lo aprendido y ponerte en modo explorador. Lo que te proponemos a continuación no son ejercicios cerrados, sino misiones de laboratorio donde tendrás que probar, deducir, justificar y enviar tus conclusiones.

Puedes resolverlas de forma individual, por parejas o en grupo. Elige los retos que tengan más sentido para tu clase: según el nivel, el tiempo disponible o el enfoque que queráis trabajar.

Ve tocando, cambiando y observando. Luego, cuando lo tengas claro, escribe tus respuestas y envíalas a tu profe desde aquí mismo.

Bloque 1: ¡Rompiendo el Hielo: Primer Contacto con el Sistema 2x2!

Misión 1.1: El Cazador de Cuadrantes

Tu misión es usar el botón “Generar Sistema Aleatorio” hasta que encuentres un sistema cuya solución P(x,y) esté en el tercer cuadrante (es decir, tanto ‘x’ como ‘y’ sean negativas). No está permitido introducir los números a mano, debes tener la paciencia de un cazador.

Pista: Utiliza el método Gráfico

✏️ Para entregar: Escribe las dos ecuaciones del primer sistema que has encontrado que cumpla la condición. y el punto de Corte P(x,y)



Misión 1.2: El Arquitecto Novato

Olvida el botón aleatorio. ¡Ahora mandas tú! Usa los controles para construir este sistema tan sencillo:
$$
\begin{cases}
x + y = 5 \\
x – y = 1
\end{cases}
$$

a) A simple vista, ¿qué dos números para x ey cumplen el sistema? ¡Seguro que lo sacas de cabeza! Anota tu predicción.

b) Comprueba tu resultado con la simulación. ¿Has acertado?

c) Ahora, crea un sistema donde la solución sea $x=2, y=2$. ¡Investiga con la simulacion hasta que lo consigas!

✏️ Para entregar:
a) El par de números (x,y) que suman 5 y restan 1
c) El sistema donde la solución sea $x=2, y=2$



Misión 1.3: El Traductor Gráfico

Con el sistema anterior ($x+y=5$, $x-y=1$), ve a la pestaña del “Método Gráfico”. La simulación te mostrará las ecuaciones en la forma explícita $y = mx + n$.

a) Para cada una, identifica claramente: ¿cuál es la pendiente ($m$)? ¿Y la ordenada en el origen ($n$)?
b) ¿La recta con pendiente negativa “cae” o “sube” hacia la derecha? ¿Y la de pendiente positiva “cae” o “sube”? Observa y anota tus conclusiones.

EcuacionesPendienteOrdenadaCae o Sube

Bloque 2: Los Tres Mosqueteros Algebraicos: "Uno para Todos y Todos para Uno

Misión 2.1 : El Arte de la Sustitución

Genera este sistema
$$
\begin{cases}
x + 2y = 8,\\
3x – y = 3.
\end{cases}
$$

a) Cópialo en tu cuaderno. Despeja la $x$ en la primera ecuación.
b) Sustituye esa expresión en la segunda ecuación y resuelve la $y$.
c) Con el valor de $y$, calcula la $x$.
d) Ahora, pide a la simulación que resuelva ese mismo sistema “paso a paso” usando el método de sustitución. ¿Tus pasos coinciden con los de la máquina? ¡Corrígete si es necesario!

✏️ Para entregar: La solucion (x,y)



Misión 2.2: El Duelo de la Igualación

Crea este sistema de ecuaciones
$$
\begin{cases}
2x + y = 7 \\
x – y = -1
\end{cases}
$$

a) Resuélvelo en tu cuaderno, pero esta vez usando el método de igualación. Elige una de la svariables para igualar
b) Comprueba tu solución y, sobre todo, tu procedimiento con la solución “paso a paso” por igualación de la simulación.

✏️ Para entregar: La solucion (x,y)



Misión 2.3: La Fuerza Imparable de la Reducción

Genera este sistema de ecuaciones

$$
\begin{cases}
5x + 3y = 8,\\
2x – y = 2.
\end{cases}
$$
a) Obsérvalo. ¿Qué incógnita parece más fácil de eliminar? ¿La $x$ o la $y$? ¿Necesitas multiplicar una ecuación o las dos?
b) Resuélvelo en tu cuaderno usando el método de reducción
c) Pide a la simulación que lo resuelva por reducción eliminando la $x$. Luego, pídele que lo haga eliminando la $y$. ¿Llegas al mismo resultado? ¿Cuál de los dos caminos te pareció más corto?

✏️ Para entregar: La incógnita mas fácil de eliminar y cual fue el camino mas corto.   Adjunta las solución del sistema (x,y)



Bloque 3: El Ojo del Geómetra: Hablando con las Rectas

Misión 3.1: El Dominador de Pendientes

Crea este sistema

$$
\begin{cases}
-x + y = 1,\\
-x + y = 3.
\end{cases}
$$

Pulsa Resolver y ve al Método Gráfico. ¿Qué observas?

Ahora utiliza los slider de la recta roja para generar rectas diferentes. Por ejemplo prueba con:
$y = x – 2$, $y = x + 5$.
a) ¿Qué observas en el gráfico cada vez que cambias solo el término $n$?
b) ¿Alguna de estas parejas de rectas llega a cortarse?
c) Conclusión del Geómetra:

Dos rectas con la misma pendiente son… ____________.

¿Qué tipo de solución tendrá un sistema formado por ellas?



Misión 4: El enigma de la Biblioteca de Pitágoras

📜 En una sala secreta de la Academia, se encontró un manuscrito codificado. Solo resolviendo el sistema correcto se abrirá la compuerta que oculta… bueno, eso tendrás que descubrirlo tú.

En el manuscrito se lee:

Ecuación 1: 3x + 5y = 7
Ecuación 2: 2x – y = 4

Pasos:

a) Resuelve el sistema en tu cuaderno usando el método que prefieras.
b) Usa la simulación para comprobarlo por otro método.
c) Representa gráficamente. ¿El punto de corte confirma tu solución?
d) Imagina que x = número de libros antiguos e y = número de compartimentos ocultos.

¿Qué interpretación tendría la solución?

📝 Para entregar:

  • Solución (x, y)
  • Método usado
  • Interpretación del resultado (¡ponle imaginación!)


Misión 5: Interceptos Reveladores – Las pistas que nadie mira

👁️ A veces, el punto de corte no habla. Pero los cortes con los ejes… esos sí. Mira donde nadie más mira y verás lo que otros se pierden.

Crea el Sistema:

2x – y = 6
x + y = 4

 📍 Pasos:

1. Ve a la pestaña “Método Gráfico”.
2. Marca la casilla “Mostrar interceptos”.
3. Observa cuidadosamente dónde cortan cada recta los ejes X e Y.

Preguntas:

a) ¿Cuáles son los puntos donde cada recta corta los ejes X e Y?
b) ¿Qué puedes deducir sobre la pendiente de cada recta solo observando esos dos puntos?
c) Si tuvieras que dibujar estas rectas a mano, ¿cómo usarías los interceptos para hacerlo rápido?
d) ¿El punto de corte del sistema está más cerca del eje X o del Y? ¿Qué significa eso?

📝 Para entregar:

  • Cuatro coordenadas: 2 cortes con ejes por recta
  • Pendiente deducida a partir de los cortes
  • Estrategia de dibujo
  • Posición relativa del punto de corte


📬 Instrucciones para enviar tus respuestas al profe

  1. Completa las actividades que te haya indicado tu profe.
  2. Haz clic en “Revisar y enviar al profe”.
  3. Revisa tus respuestas. Si necesitas corregir algo, pulsa “❌ Corregir”.
  4. Cuando estén bien, haz clic en “📋 Copiar respuestas”.
  5. Luego pulsa “📬 Abrir Gmail” y pega las respuestas en el correo.
  6. Escribe el asunto y el email del profe, y pulsa Enviar.

🛡️En AulaQuest no se guarda nada. Tus respuestas no se almacenan, no se asocian a tu cuenta y nadie más las verá. Es solo un canal directo y privado entre tú y tu profe.

📚 Zona Profe – Acceso exclusivo para docentes
Bienvenido a la Zona Profe. Aquí encontrarás las soluciones detalladas de las actividades propuestas para tus estudiantes. Cada una ha sido elaborada con rigor y cuidado, basándonos en los datos del simulador y principios físicos sólidos.

Eso sí, aunque revisamos todo con atención, puede colarse alguna imprecisión. Te recomendamos que, antes de usar estas soluciones para corregir o explicar en clase, verifiques los cálculos por si acaso. Gracias por tu confianza y por hacer de la ciencia algo emocionante.

🔒 Esta solución está disponible solo para docentes registrados.

¿Eres profe? Solicita acceso aquí para desbloquear los recursos exclusivos.

💥 ¿Has creado una actividad que ha hecho brillar los ojos de tus alumnos?

¿Un experimento que dejó a tu clase con la boca abierta?
¿Una forma única de explicar ese tema que siempre se atraganta?

🎓 No lo guardes solo para ti. Súbela, compártela, inspíranos.

En AulaQuest creemos que la educación se transforma compartiendo, no compitiendo.
Cada actividad que subes no es solo un recurso: es una chispa que puede encender la pasión por aprender en otra aula, en otro colegio, en otra parte del mundo.

💡 Si tu actividad nació a partir de una de nuestras simulaciones, cuéntalo.
🔥 Porque tu experiencia puede abrir caminos.
🌍 Y tu creatividad puede cruzar fronteras.

Simulaciones en Física