Simulador Movimiento Armónico Simple (MAS - MCU)
🎵 Simulador de Movimiento Armónico Simple (MCU-MAS)
El movimiento armónico simple (MAS) es una de las bases más importantes de la física de oscilaciones.
Surge al proyectar un movimiento circular uniforme (MCU) sobre un eje, generando una oscilación sinusoidal
que sigue la ecuación y = A·sen(ωt + φ).
En este simulador interactivo de MAS podrás visualizar cómo un objeto que gira en círculo se traduce en una vibración periódica,
comprendiendo de forma clara la relación entre MCU y MAS. Es una herramienta ideal para estudiantes y docentes que buscan un
laboratorio virtual de física accesible y práctico.
¿Quieres seguir explorando oscilaciones y sistemas elásticos? Descubre también:
📋 Detalles de la simulación
- 🔗 Categoría: Física | Ondas y Sonido ↗️
- 🎓 Nivel educativo: ESO
- ⚙️ Dificultad: Fácil (3/10)
- 📈 Visitas: 77
×
📎 Código para incrustar
¿Eres profe, divulgador o webmaster?
Puedes incrustar esta simulación en tu web o blog sin problema.
Solo pedimos dos cosas básicas:
- ✅ Que cites la fuente: AulaQuest.com
- 🚫 Que no la uses con fines comerciales
Este es el código que puedes copiar:
<iframe
src="https://aulaquest.github.io/mcu-mas/"
width="100%"
height="560"
style="border: 1px solid #ccc; border-radius: 8px;"
allowfullscreen
title="Simulador Movimiento Armónico Simple (MAS - MCU)"></iframe>La Sombra de un Círculo: Conectando MCU y MAS
Hola a todos los estudiantes de Aula Quest. Bienvenidos a esta exploración dedicada. Hoy nos metemos de lleno en un tema, bueno, un tema central de la física: el Movimiento Armónico Simple, que abreviaremos como MAS.
Pero atención, no vamos a repasarlo como si fuera un libro de texto, ¿eh? Vamos a descubrir juntos una conexión visual increíblemente potente y, francamente, bastante sorprendente con otro movimiento: el Movimiento Circular Uniforme, el MCU.
Precisamente. A menudo se enseñan como dos capítulos separados, pero la realidad es que entender cómo el MAS es, en esencia, una... una consecuencia visible del MCU cambia bastante la perspectiva. Es una forma muy, muy intuitiva.
Y lo mejor de todo es que tenéis una herramienta genial justo ahí al lado. Esa simulación interactiva no es un adorno, para nada. La idea es que mientras charlamos, podáis, eh, tocar los controles, cambiar valores como la amplitud o el periodo y ver en tiempo real qué efecto tiene sobre el movimiento. Es aprender haciendo.
Exacto. Vamos a usar esa simulación para desgranar los conceptos clave: la ecuación que lo describe todo, qué significan sus partes y cómo la posición, la velocidad y la aceleración de la partícula que oscila están relacionadas en una especie de, bueno, de danza cósmica perfectamente sincronizada, aunque no siempre vayan al mismo paso, ¿eh?
Así que, preparad esos controles deslizantes, ¿listos para ver la física cobrar vida? Pues vamos allá. Empecemos por lo básico: ¿qué imagen nos viene a la cabeza con MAS? Típicamente, algo que va y viene, ¿no?, que oscila de forma regular.
Ese movimiento periódico genera una gráfica de posición frente al tiempo muy especial, esa onda tan característica, una sinusoide.
Y aquí viene la conexión clave, la que muchas veces no se visualiza de entrada. Ese movimiento de vaivén, esa oscilación, se puede entender a la perfección si imaginamos un objeto dando vueltas en círculo a velocidad constante —eso es el MCU— y nos fijamos únicamente en su sombra proyectada sobre una línea recta, por ejemplo, un eje vertical.
Esto es lo que tenéis que probar ahora mismo en la simulación. Fijaos bien. La partícula verde está en pleno MCU, girando sin parar. Ahora mirad la partícula amarilla, que está justo en la línea vertical.
Es su proyección.
Es, literalmente, la sombra o proyección vertical de la verde. ¿Y qué hace la amarilla? Sube y baja, sube y baja. Ese movimiento de la sombra es un MAS puro. Es... es alucinante ver cómo algo tan simple como un giro constante se traduce en esta vibración.
Sí, sí, la verdad es que verlo así es una pasada.
Verlo así, en directo, es mucho más potente que leerlo en un libro, desde luego.
Totalmente. Es una revelación visual, ¿verdad? Y define la naturaleza matemática del MAS. La posición de esa sombra amarilla varía con el tiempo siguiendo una función seno o coseno.
La propia forma de la gráfica que se dibuja en la simulación para la posición de la partícula amarilla es una onda sinusoidal perfecta. Esa conexión círculo-sombra-onda es, es fundamental.
Y claro, si hay una onda sinusoidal, tiene que haber una ecuación matemática que la describa. Aquí es donde entra la fórmula maestra del MAS. A ver, puede parecer intimidante al principio con letras griegas y demás, pero vamos a desmontarla pieza a pieza.
Venga. La ecuación es:
$$
y(t) = A \sin(\omega t + \phi)
$$
Tranquilos, vamos a ver qué es cada símbolo y cómo se relaciona con lo que veis en la simulación.
Empecemos por la $A$, la amplitud. Esta es, quizás, la más fácil de visualizar, ¿no?
Sí, yo creo que sí. Representa simplemente la elongación máxima, es decir, cuánto se aleja la partícula amarilla de su posición central de equilibrio en su viaje de subida y bajada. $y$ es la posición en cualquier instante y $A$ es el valor máximo que alcanza esa $y$.
Probadlo en la simulación. Buscad el control llamado "Radio (m)". Ese radio del círculo que describe la partícula verde es, eh, exactamente la amplitud ($A$) del MAS de la partícula amarilla.
Aumentad el valor del radio. ¿Qué pasa?
Pues que el círculo se hace más grande.
¡Claro! Y la partícula amarilla viaja más arriba y más abajo, su recorrido es mayor. Y la onda dibujada en la gráfica se hace más alta. Sus crestas y valles se separan más del eje central. Esa altura de la onda es la amplitud.
Muy bien observado. El siguiente ingrediente es $\omega$, omega. Esta letra griega representa la pulsación o frecuencia angular. Nos dice, eh, cómo de rápido se produce la oscilación.
La rapidez, vale.
Técnicamente, mide cuántos radianes recorre el movimiento circular asociado por cada segundo que pasa. Está íntimamente ligada al tiempo que tarda la partícula en hacer una oscilación completa: subir, bajar y volver al punto inicial, que llamamos periodo ($T$).
La relación es, bueno, es sencilla:
$$
\omega = \frac{2\pi}{T}
$$
Tiene sentido. $2\pi$ radianes es una vuelta completa del círculo, ¿no?
Exacto. Entonces, si el periodo $T$ es pequeño (tarda poco en dar la vuelta), entonces $\omega$ será grande, recorre muchos radianes por segundo y la oscilación será muy rápida.
Cambiad el valor del "Periodo (s)" en la simulación. Si lo hacéis más pequeño...
¡Zas! Todo se acelera.
¡Exacto! Esa $\omega$, calculada a partir del periodo que fijamos, es como la marcha a la que funciona todo el sistema.
Y nos queda el último término dentro del seno: $\phi$, fi. Este concepto a veces cuesta un poco más al principio.
Sí, este es el que lía a veces.
Básicamente, nos indica en qué estado se encontraba el movimiento justo cuando empezamos a medir el tiempo, o sea, en $t=0$. La partícula amarilla, ¿empezó desde el centro ($y=0$) y subiendo? ¿Empezó desde arriba del todo ($y=A$)? ¿O desde algún punto intermedio? La fase inicial ajusta ese punto de partida.
Entiendo. Es como el ángulo inicial desde el que parte la partícula verde en su círculo antes de que pongamos el cronómetro en marcha, ¿no?
Justo eso. Jugad con el control de "Fase ($\phi$)" en la simulación. Si está a cero, al reiniciar, la partícula amarilla arranca desde $y=0$ y empieza a subir. Ahora moved ese deslizador.
¿Veis cómo toda la onda en la gráfica se desplaza horizontalmente, a izquierda o derecha? Ese desplazamiento es el efecto de la fase inicial.
Eso es. Cambiar la fase inicial es como darle una ventaja o un retraso a la partícula en su ciclo.
Exactamente, esa es la idea. La fase inicial $\phi$ nos dice el ángulo de partida en el círculo asociado. Y con estos tres parámetros: amplitud $A$ (tamaño de la oscilación), pulsación $\omega$ (rapidez de la oscilación) y fase inicial $\phi$ (punto de partida en el ciclo), podemos describir matemáticamente cualquier MAS que nos encontremos.
Vale. Esto aclara bastante la ecuación. Pero espera, hay algo que a mí siempre me liaba un poco en clase, ¿eh? A veces ves la ecuación del MAS escrita con la función coseno en lugar de seno: $y = A \cos(\omega t + \phi)$. ¿Es un error? ¿Son cosas distintas? ¿Cuál usamos?
Es una duda muy común, sí. Y la respuesta corta es: ambas son perfectamente válidas. Describen el mismo fenómeno físico, un movimiento armónico simple. La diferencia fundamental está en la, digamos, la convención sobre dónde se considera que empieza el movimiento cuando la fase inicial es cero.
Ah, vale. O sea, dónde ponemos el $t=0$.
Exacto. Si usamos $y = A \sin(\omega t)$ y ponemos $\phi=0$, estamos describiendo un movimiento que en $t=0$ está en la posición de equilibrio, $y=0$, y empieza a moverse hacia valores positivos, hacia arriba en nuestra simulación.
Vale.
En cambio, si usamos $y = A \cos(\omega t)$ y ponemos $\phi=0$ en esa fórmula con coseno, describimos un movimiento que en $t=0$ ya está en la máxima elongación positiva, $y=A$, listo para empezar a bajar.
Entendido.
La relación matemática es que la función coseno está simplemente desfasada $\pi/2$ radianes, o sea, 90 grados, respecto a la función seno. Es decir:
$$
\cos(x) = \sin(x + \frac{\pi}{2})
$$
Y aquí es donde la fase inicial $\phi$ en nuestra fórmula general con seno, $y = A \sin(\omega t + \phi)$, se vuelve tan útil. Nos da la flexibilidad de ajustar ese punto de partida como queramos.
Vamos a comprobarlo en la simulación. Aseguraos de que la fase $\phi$ está en cero. Veréis la típica onda seno que empieza en el origen, ¿verdad?
Sí, la que sale por defecto.
Ahora, ajustad la fase a $\pi/2$, que es más o menos 1.57 radianes. Mirad la gráfica. Ahora empieza desde el máximo. Se ha transformado en una onda coseno.
Justo. Por eso, la fórmula con seno y el parámetro $\phi$ es más general. Ajustando $\phi$ podemos representar cualquier MAS, sin importar si empieza en el centro, en un extremo o en cualquier punto intermedio.
Justo eso. Así que no hay que preocuparse si se encuentra la fórmula con coseno. Simplemente es una elección diferente del origen de fases, que es totalmente equivalente a usar $\phi = \pi/2$ en la fórmula del seno.
Entendido. Oye, hemos hablado de la pulsación $\omega$ y del periodo $T$, pero hay otro término que siempre aparece en estos temas: la frecuencia $f$. A veces puede parecer un lío tener tres nombres para hablar de la rapidez del movimiento. ¿Podemos aclarar un poco la relación entre $T$, $f$ y $\omega$?
Claro, es importante tenerlos claros porque, aunque relacionados, no son lo mismo. Los tres nos hablan de lo rápido que oscila el sistema, pero cada uno lo hace de una manera ligeramente distinta. El periodo $T$, como hemos dicho, es el tiempo que tarda en completarse una oscilación. Se mide en segundos.
Vale, el tiempo por vuelta. Es el control "Periodo (s)" de la simulación. Si lo aumentas, el movimiento se vuelve más lento, tarda más en hacer un ciclo completo.
Eso es. La frecuencia $f$ es conceptualmente lo contrario al periodo. Nos dice cuántas oscilaciones completas ocurren en un segundo. Se mide en Hertz (Hz), que significa ciclos por segundo.
Ah, la inversa.
Exacto. La relación es muy simple:
$$
f = \frac{1}{T}
$$
Si en la simulación pones $T=2$ segundos, la frecuencia será $f = 1/2 = 0.5$ Hz, medio ciclo cada segundo. Un periodo corto implica una frecuencia alta y viceversa.
Lógico.
Y volvemos a la pulsación o frecuencia angular $\omega$. Es la que usamos directamente en la ecuación seno/coseno. Mide la velocidad angular del movimiento circular asociado, en radianes por segundo. Su relación con el periodo es $\omega = 2\pi/T$.
Otra vez el $2\pi$.
Claro, el $2\pi$ viene de que una vuelta completa son $2\pi$ radianes. Así, mientras $T$ nos da segundos por ciclo y $f$ nos da ciclos por segundo, $\omega$ nos da radianes por segundo. Es la "traducción" que necesitan las funciones trigonométricas para describir el ángulo que se recorre.
Y en la simulación, si os fijáis, hay un indicador del ángulo total que ha girado la partícula verde, llamado $\theta$. Este ángulo simplemente va aumentando con el tiempo según $\theta = \omega t$, si la fase inicial $\phi$ es cero. Así que $\omega$ es realmente la velocidad a la que gira ese ángulo, ¿no? Es lo que impulsa todo el movimiento.
Precisamente. $T$, $f$, $\omega$: tres caras de la misma moneda, el ritmo de la oscilación.
Muy bien. Creo que la posición $y$ y cómo depende del tiempo ya está bastante más clara. Pero, claro, la partícula amarilla no solo está en sitios, también se mueve con una cierta velocidad y está sometida a una aceleración. ¿Cómo varían estas magnitudes durante la oscilación? Porque no son constantes, ¿verdad?
Para nada. Ahí entramos en la dinámica del MAS. Y es muy interesante, porque a diferencia de movimientos más simples, ni la velocidad ni la aceleración son constantes. Varían continuamente.
Matemáticamente, bueno, se obtienen derivando la posición respecto al tiempo. Si partimos de $y(t) = A \sin(\omega t + \phi)$, la velocidad $v(t)$ resulta ser $A\omega \cos(\omega t + \phi)$. Fíjate que aparece un coseno y la pulsación $\omega$ multiplicando a la amplitud.
Vale. $A\omega\cos(...)$
Y la aceleración $a(t)$, si derivamos de nuevo, es $-A\omega^2 \sin(\omega t + \phi)$. Aquí vuelve el seno, pero con un signo negativo y, ojo, $\omega^2$.
$-A\omega^2\sin(...)$ O sea, que vuelve a ser proporcional a $y$.
Exacto. Una forma compacta y muy importante de escribir esto es:
$$
a(t) = -\omega^2 y(t)
$$
Esta relación, que la aceleración sea proporcional y opuesta a la posición, es la definición dinámica fundamental del MAS. Es lo que causa el movimiento armónico.
Las fórmulas son útiles, pero ¿qué implican en la práctica? ¿Qué le pasa a la partícula amarilla? Pensemos en su velocidad. ¿Dónde se mueve más rápido?
Pues... intuitivamente parece que coge impulso al pasar por el centro, $y=0$. Y así es. La velocidad es máxima justo en el punto de equilibrio.
Claro, ahí es donde menos "freno" o "empuje" hay de la fuerza restauradora.
Y en cambio, cuando llega a los extremos ($y=A$ o $y=-A$), tiene que pararse un instante para cambiar de dirección, ¿no?
Justo. Ahí la velocidad es cero, se detiene momentáneamente.
Vale. ¿Y la aceleración?
Pues la aceleración va un poco a la contra de la velocidad. Es cero justo en el centro, $y=0$, donde la velocidad es máxima. Ahí no hay fuerza neta empujando o frenando. Pero en los extremos, $y=A$ y $y=-A$, donde la velocidad es cero...
Ahí es máxima.
Ahí la aceleración es máxima, sí. Y lo importante es que siempre apunta hacia el centro. Si la partícula está arriba, la aceleración tira para abajo. Si está abajo, tira para arriba. Es la responsable de que el movimiento se invierta, actúa como una fuerza restauradora constante hacia el equilibrio.
Y esto es oro puro para verlo en la simulación. Id al menú desplegable "Gráfica". Cambiad de "Posición (y)" a "Velocidad (v)". Aparece otra onda, ¿veis? Es cosenoidal, si $y$ era seno.
Fijaos en los picos.
Mirad los picos de velocidad. Coinciden justo cuando la posición $y$ pasa por cero. Y la velocidad es cero cuando la posición es máxima o mínima.
Está desfasada 90 grados.
Ahora poned la gráfica en "Aceleración (a)". Otra onda más. Sus valores máximos, en magnitud, claro, ocurren en los extremos, igual que la posición, pero con signo contrario. Y la aceleración es cero cuando la posición es cero.
Justo donde la velocidad era máxima.
Y el remate final: elegid "Todo". Se ven las tres gráficas juntas: posición, velocidad y aceleración. Es fascinante ver el desfase entre ellas.
Es como un baile, ¿verdad?
Totalmente. La velocidad va 90 grados ($\pi/2$) por delante de la posición. La aceleración va otros 90 grados por delante de la velocidad. Eso es 180 grados ($\pi$) respecto a la posición. Por eso está invertida respecto a $y$.
Es un ballet perfectamente coreografiado. Entender esto es clave.
Comprender esos desfases es crucial, sí. Saber que cuando la posición es máxima, la velocidad es cero y la aceleración es máxima pero negativa. Y que cuando la posición es cero, la velocidad es máxima y la aceleración es cero. Eso es entender la esencia dinámica del MAS.
Ya casi terminamos. Solo una pequeña curiosidad que también se puede explorar con la simulación. ¿Influye si la partícula verde, la del MCU, gira en sentido antihorario (como hace por defecto) o en sentido horario?
Es una pregunta interesante sobre la simetría del sistema. Y sí, sí que influye, aunque el efecto depende un poco de la fase inicial que tengamos puesta.
Ah, vale.
Cambiar a sentido horario es como usar una pulsación $\omega$ negativa en las ecuaciones que hemos visto.
Poner un menos delante de $\omega$.
Exacto. Si la fase inicial $\phi$ es cero, la posición es $y(t) = A \sin(\omega t)$. Si cambiamos a horario, sería $y(t) = A \sin(-\omega t)$. Como la función seno es impar, recuerda, $\sin(-x) = -\sin(x)$, la gráfica simplemente se invierte verticalmente. Empieza hacia abajo en lugar de hacia arriba.
Vale, se da la vuelta.
Pero, haced esta prueba curiosa: poned la fase $\phi$ en $\pi/2$, o sea, 1.57 radianes. Recordad que esto hacía que la gráfica de posición empezara como un coseno, desde $y=A$, ¿verdad?
Sí, empezaba desde el máximo.
Ahora, mantened esa fase y cambiad el sentido de giro entre antihorario y horario. Mirad atentamente la gráfica de posición $y$. ¿Notáis algún cambio?
Pues... no, ¿verdad? No cambia. La gráfica es idéntica.
Exacto. ¿Por qué pasa esto?
Pues, porque con $\phi = \pi/2$, la posición se describe realmente con un coseno: $y(t) = A \sin(\omega t + \pi/2)$, que es igual a $A \cos(\omega t)$. Y la función coseno es par.
Ah, claro, $\cos(-x) = \cos(x)$.
¡Eso es! Así que cambiar el signo de $\omega$ (cambiar el sentido de giro) no afecta al resultado en este caso específico de empezar desde el extremo. Es una pequeña, bueno, una peculiaridad matemática que la simulación nos deja ver claramente. Curioso, ¿eh?
Muy curioso, la verdad. Y con esto pues cerramos nuestra exploración de hoy. Para mí, lo más potente ha sido visualizar tan nítidamente cómo ese vaivén aparentemente simple del MAS surge de algo tan fundamental como un giro constante.
Esa idea de la sombra o proyección es, es una herramienta mental muy poderosa.
Estoy de acuerdo. Hemos diseccionado la ecuación $y = A \sin(\omega t + \phi)$ y ahora entendemos mejor qué representan la amplitud $A$ (el alcance del movimiento), la pulsación $\omega$ (el ritmo, que está conectada a $T$ y $f$) y la fase inicial $\phi$ (el punto de partida angular).
Y hemos visto el baile desfasado de la velocidad y la aceleración respecto a la posición.
Confiamos en que esta conversación y, sobre todo, el haber podido trastear con la simulación mientras escuchabais, os haya ayudado a consolidar estas ideas. Ahora la clave es seguir jugando con ella, cambiad la amplitud, el periodo, la fase y observad. No hay mejor manera de interiorizar la física que experimentando.
Sin duda. Y un último pensamiento para llevarse. Este MAS, aunque lo hayamos derivado de un círculo ideal, no es solo un modelo matemático bonito que se queda en los libros. Es increíblemente fundamental en la naturaleza.
Resulta que muchísimas cosas en el universo real oscilan o vibran de una manera muy, muy parecida a un MAS, al menos como primera aproximación.
Exacto. Piensa en la vibración de una cuerda de guitarra generando sonido, las moléculas de aire transmitiendo ese sonido como ondas de presión, los campos eléctricos y magnéticos en una onda de luz o de radio, incluso los átomos vibrando en la red de un cristal.
Todos ellos exhiben comportamientos oscilatorios que podemos empezar a entender gracias a este modelo tan simple, el MAS. Así que, como reflexión final, si este patrón de vaivén sinusoidal es tan común, ¿qué ocurrirá cuando varios de estos movimientos se combinen o interfieran entre sí?
¡Uf! Ahí ya entramos en el fascinante mundo de las ondas complejas, la superposición, las resonancias...
Exacto. Ahí es donde la física de las ondas y las vibraciones abre puertas a fenómenos aún más complejos y, bueno, fascinantes. Algo en lo que pensar. Gracias por habernos acompañado en esta inmersión en el MAS a través del MCU. Hasta la próxima exploración en Aula Quest.
¿Qué es el M.A.S. y cómo se relaciona con el Movimiento Circular?
El Movimiento Armónico Simple (M.A.S.) es un movimiento oscilatorio de vaivén, como el de un péndulo. Su rasgo distintivo es que su posición a lo largo del tiempo se describe con una onda sinusoidal (seno o coseno).
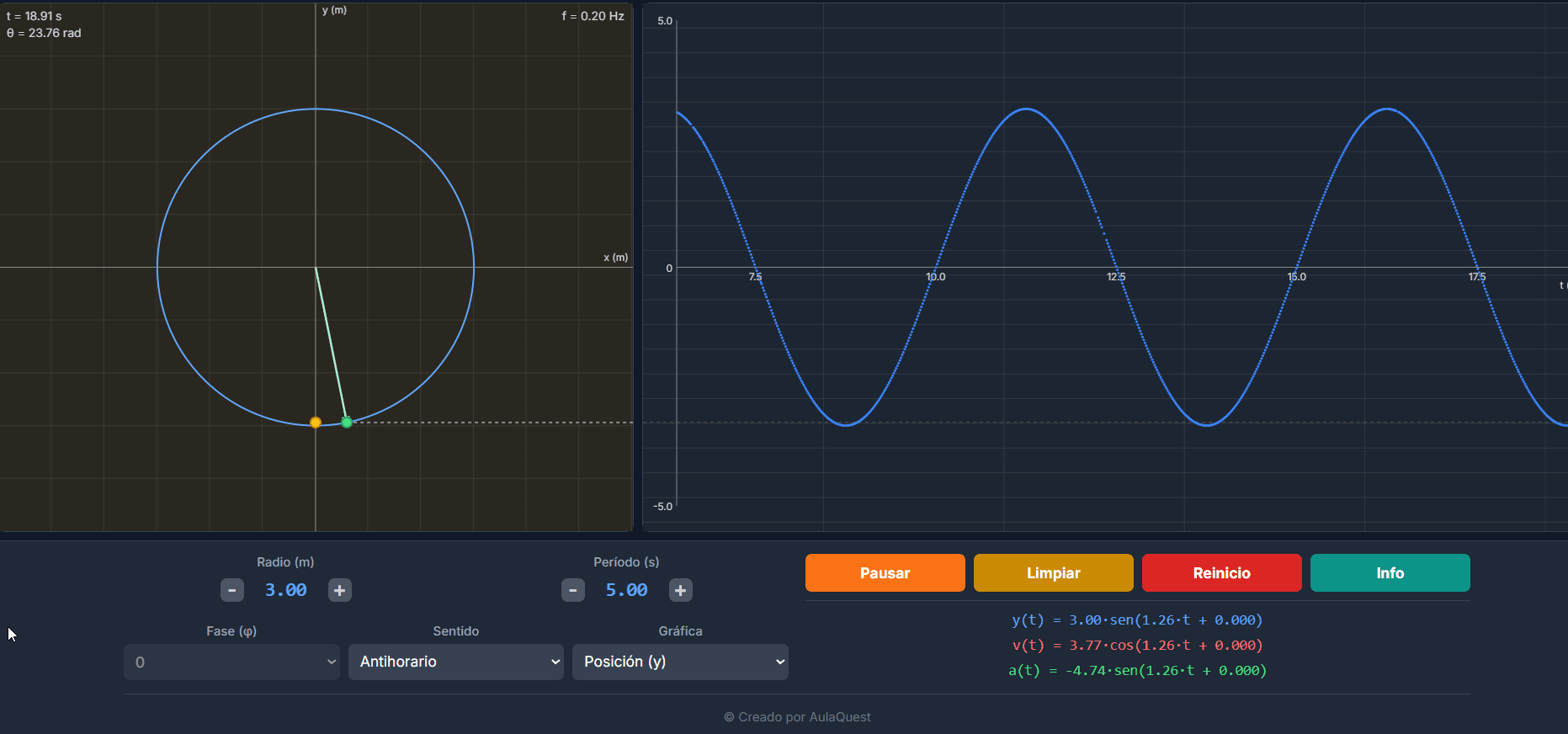
La conexión fundamental, que este simulador demuestra, es que el M.A.S. puede entenderse como la proyección de un Movimiento Circular Uniforme (M.C.U.) sobre un eje. En el simulador, la partícula verde realiza un M.C.U. y su "sombra" vertical (la partícula amarilla) ejecuta un M.A.S., ilustrando cómo un giro se traduce en una vibración.
¿Qué se entiende por "elongación" y "amplitud"?
La elongación (y) es la distancia a la que se encuentra la partícula de su posición de equilibrio en cualquier instante. Es un valor que cambia constantemente.
La Amplitud (A) es el valor máximo de la elongación. Es la distancia desde el centro hasta uno de los extremos. En el simulador, la Amplitud del M.A.S. es exactamente el Radio (m) del círculo. ¡Modifícalo y verás cómo cambia el alcance del movimiento!
¿Qué representan los términos en la ecuación y(t) = A·sen(ωt + φ)?
Cada término en la ecuación fundamental del M.A.S. tiene un significado físico crucial que puedes controlar en el simulador:
- A (Amplitud): Como vimos, es la máxima elongación y equivale al Radio (m).
- ω (Pulsación o Frecuencia Angular): Mide la velocidad de la oscilación en radianes por segundo. Se calcula como ω = 2π / T. Es el "motor" que impulsa el movimiento.
- φ (Fase Inicial): Determina el "punto de partida" del movimiento en t=0. Manipulando la Fase (φ) en el simulador, puedes desplazar la onda horizontalmente.
¿Por qué se usan seno y coseno para describir el M.A.S.?
Ambas funciones son válidas, ya que solo se diferencian en su punto de inicio. Una función seno describe un movimiento que empieza en la posición de equilibrio (y=0), mientras que una función coseno describe uno que inicia en la máxima amplitud (y=A).
La función coseno es simplemente una función seno desfasada π/2 radianes (90°). La clave está en la Fase Inicial (φ). Si ajustas φ a π/2 en una ecuación con seno, obtienes una gráfica idéntica a la de un coseno. Por eso, la fórmula con seno y fase es la más completa.
¿Qué relación hay entre Período, Frecuencia y Pulsación (ω)?
Estos tres conceptos describen la "rapidez" de la oscilación y están conectados:
- Período (T): Es el tiempo en segundos de una oscilación completa. Es el control principal en el simulador para ajustar la velocidad.
- Frecuencia (f): Es la inversa del período (f = 1/T) y mide cuántas oscilaciones se realizan por segundo (en Hertz, Hz).
- Pulsación o frecuencia angular (ω): Es la velocidad angular (rad/s). Se calcula como ω = 2π / T y es el valor que aparece en la ecuación del M.A.S.
Observa el ángulo total (θ = ωt) en el simulador: muestra cómo la pulsación por el tiempo genera tanto el movimiento circular como la onda sinusoidal.
¿Cómo se relacionan posición, velocidad y aceleración en el MAS y el MCU?
Este simulador muestra cómo un Movimiento Circular Uniforme (MCU) se proyecta sobre un eje para generar un Movimiento Armónico Simple (MAS) usando la función seno para la elongación.
y(t) = A·sen(ωt + φ)
v(t) = A·ω·cos(ωt + φ)
a(t) = -A·ω²·sen(ωt + φ)
En el MCU, la velocidad angular ω es constante y la aceleración centrípeta apunta al centro del círculo. Cuando proyectamos este movimiento sobre un eje, obtenemos el MAS, donde:
- La posición oscila entre +A y -A siguiendo un seno.
- La velocidad es máxima al pasar por el centro y cero en los extremos.
- La aceleración es máxima en los extremos (hacia el centro) y cero en el centro.
Así, aunque la velocidad en el MCU sea constante, la proyección sobre un eje genera las oscilaciones características del MAS.
¿Afecta el sentido de giro del M.C.U. al M.A.S. resultante?
Sí, de forma sutil. El sentido Antihorario es la convención estándar. Cambiar a Horario es como si la pulsación (ω) se volviera negativa, lo que puede invertir la gráfica de posición si φ=0.
Sin embargo, si la fase inicial se fija en π/2 (empezando en el punto más alto), cambiar el sentido de giro no altera la gráfica de posición, debido a las propiedades de simetría de la función coseno.
¿Cuál es el propósito de este simulador?
El propósito principal es ofrecer un laboratorio virtual de física para entender la conexión entre el Movimiento Circular Uniforme y el Armónico Simple. Permite manipular parámetros como amplitud, pulsación y fase para observar sus efectos directos en las gráficas de posición, velocidad y aceleración, facilitando así la comprensión de las bases de la física de oscilaciones.
Zona de Actividades de tu Profesor
Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.
¿Tu última clase con la simulación fue un éxito?
Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Crear una actividad es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.
- 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
- 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
- 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
📤 Subir mi actividad
*Esto es solo para profes. Si lo eres, pide tu acceso.
Otras Simulaciones en Física
