Laboratorio de Parábolas

🎯 Simulador de parábolas: más que una simple curva

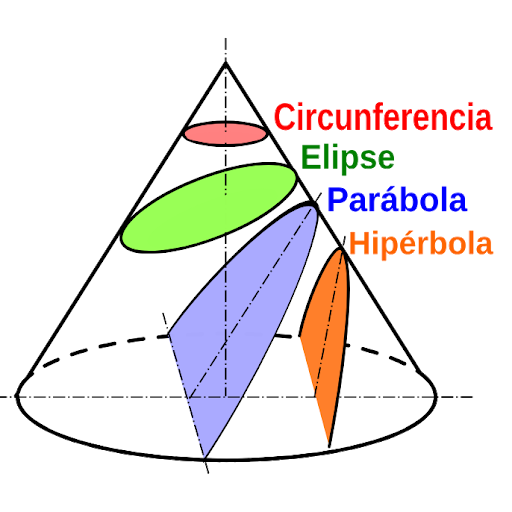
La parábola es una de las figuras más fascinantes de la geometría. Forma parte del clan de las cónicas, junto a la elipse y la hipérbola. Se obtiene al cortar un cono con un plano paralelo a una de sus generatrices.

En este simulador de parábolas vas a jugar con sus coeficientes, mover el vértice, descubrir raíces, entender la simetría y ver por qué esta curva tiene más miga de lo que parece. Y lo harás como se hace en AulaQuest: explorando, tocando y comprendiendo.

📋 Detalles de la simulación

  • 📂 Categoría: cónicas
  • 🎓 Nivel educativo: ESO
  • ⚙️ Dificultad: Media
  • 📈 N.º de veces usada: 58
Ver en pantalla completa

Desmontando la Parábola: De la Ecuación a las Antenas

¡Hola a todos los estudiantes de AulaQuest! ¿Listos? Hoy vamos a, eh, sumergirnos en una figura geométrica que seguro que os suena: la parábola. Sí, esa curva cónica, ¿verdad? Que sale de cortar un cono, como la elipse o la hipérbola.
Pero lo curioso es que está por todas partes. Totalmente, en física, en mates, ingeniería, mmm, la trayectoria de una pelota, hasta en las antenas.
Exacto. Y la pregunta es, ¿por qué esa forma? ¿Qué tiene de especial? Pues hoy vamos a investigar justo eso. Vamos a conectar la teoría, las fórmulas, con las simulaciones interactivas que tenéis ahí delante.
La idea es, bueno, que no sea solo memorizar, sino ver cómo funciona. Precisamente. Que se vea esa conexión, ¿no? Entre los símbolos, el álgebra, y lo que pasa en la pantalla cuando movemos algo. Que la intuición visual acompañe.
Pues venga, entremos en materia. La forma quizá más habitual, la de bachillerato, es: $$ y = ax^2 + bx + c $$ ¿Qué nos cuentan esas letras? $a$, $b$ y $c$.
Pues son, eh, son la clave de todo, la verdad. El coeficiente $a$, por ejemplo, nos dice dos cosas importantes. A ver. Primero, si la parábola se abre hacia arriba, como una sonrisa, si $a$ es positivo ($a > 0$), o hacia abajo, si $a$ es negativo ($a < 0$).
Y segundo, controla cómo de ancha o estrecha es. Ah, o sea, la apertura y la... la forma, digamos. Eso es. Una $a$ grande en valor absoluto, $|a|$, hace la parábola más estrechita. Si es pequeña, se ensancha. Y eso, bueno, se ve genial jugando con $a$ en la Simulación 1.
Vale, vale. La $a$ controla la forma básica. ¿Y la $b$? Esa siempre me ha parecido menos... menos directa. Es verdad, $b$ es más sutil, ¿eh? Influye en dónde se sitúa el vértice horizontalmente.
Y claro, como el vértice marca el eje de simetría, pues también afecta al eje. Entonces, al cambiar $b$ en la Simulación 1, ¿la movemos de lado? Sí, la desplaza lateralmente, pero ojo, no es solo eso.
Al cambiar $b$, el vértice se mueve, y como la $y$ del vértice depende de $x$, pues también cambia la altura. No es un simple movimiento horizontal, ¿sabes? Es un pelín más complejo.
Mmm, interesante esa combinación. ¿Y $c$? Esa parece más fácil, ¿no? Sí, $c$ es bastante más directa. Es el término independiente. Nos dice, sin más, a qué altura corta la parábola el eje $y$. El punto $(0, c)$.
Ah, claro. Si cambias $c$ en la simulación, verás que toda la parábola sube o baja verticalmente, sin cambiar ni forma ni posición horizontal. Probadlo en la Simulación 1, que es muy claro.
Vale, perfecto. Coeficientes entendidos. Hablemos ahora de puntos importantes. El vértice. Ese punto mínimo o máximo, ¿no? Justo. El punto más bajo si la parábola va hacia arriba ($a>0$) o el más alto si va hacia abajo ($a<0$).
Y hay una formulita muy útil para su coordenada $x$. La de: $$ x = -\frac{b}{2a} $$ ¿verdad? En la ecuación $y = ax^2+bx+c$ y sacas la coordenada $y$.
Que, por cierto, esa fórmula viene de buscar dónde la derivada es cero, ¿no? Un pequeño guiño al cálculo. Exacto, un pequeño spoiler de lo que viene después.
Y aparte del vértice, están las raíces o los ceros que también se llaman, los cortes con el eje $x$. Eso es. Son los puntos donde la $y$ vale 0. Para encontrarlos, pues, hay que resolver la ecuación: $$ ax^2 + bx + c = 0 $$
La famosa ecuación de segundo grado. La misma. Y aquí pueden pasar tres cosas, claro: que tengamos dos raíces (dos puntos de corte)... O una sola raíz, si el vértice justo toca el eje $x$. Exacto, una raíz doble se llama.
O que no haya ninguna raíz real. Eso pasa si la parábola está entera por encima o por debajo del eje $x$, sin llegar a cortarlo. Y todo esto, vértice, raíces, está conectado por el eje de simetría.
Esa línea vertical que parte la parábola en dos mitades iguales. Justo, la recta vertical $x = -\frac{b}{2a}$, que pasa, cómo no, por el vértice. Y la Simulación 2 nos ayuda a visualizar todo esto, entiendo.
Sí, la Simulación 2 es genial para eso. Te marca el vértice, las raíces (si las hay), el eje, y puedes cambiar $a, b, c$ y ver cómo se mueve todo junto. Es... es ver la maquinaria funcionando.
Muy bien, pero, eh, ¿hay otra manera de definir la parábola, no? Una definición más... geométrica. Que tiene que ver con un foco y una directriz.
¡Ah, sí! Esa es una definición preciosa y muy potente. Geométricamente, una parábola es el conjunto de todos los puntos que están exactamente a la misma distancia de un punto fijo, llamado foco, y de una recta fija, llamada directriz.
Misma distancia a un punto y a una recta... ¿Y esa para qué sirve? ¡Uf! Pues para muchísimo. Esa propiedad es la base del funcionamiento de las antenas parabólicas, por ejemplo, o de los faros de los coches.
¿Cómo? A ver, explica eso. Pues mira, cualquier rayo de luz, de sonido, de señal de satélite que llegue a la parábola paralelo a su eje de simetría, ¡pum!, se refleja y pasa por el foco. Todos convergen ahí.
Ostras, ¡concentra la señal! Exacto. Y al revés, si pones una bombilla en el foco, los rayos de luz salen reflejados en la parábola y forman un haz paralelo. Por eso los faros iluminan lejos.
Qué bueno. ¿Y esta definición geométrica tiene su propia ecuación? Sí, claro. Es la llamada forma canónica. Si el vértice está en $(h,k)$ y la parábola se abre verticalmente, la ecuación es: $$ y = \frac{1}{4p}(x-h)^2 + k $$
Vale, $(h, k)$ es el vértice, eso ya lo teníamos. ¿Y qué es $p$? $p$ es la distancia del vértice al foco y a la directriz. Si $p$ es positiva, el foco está por encima del vértice y la parábola se abre hacia arriba. Si $p$ es negativa, el foco está debajo y se abre hacia abajo.
Y la Simulación 3, imagino que va de esto. Justo. En la Simulación 3 se puede jugar con $h$, $k$ y $p$. Se ve cómo se mueven el vértice, el foco, la directriz y, lo más importante, se puede comprobar que cualquier punto que elijas de la parábola cumple eso de estar a la misma distancia del foco y de la directriz.
Fascinante ver cómo esa propiedad, puramente geométrica, genera la curva que ya conocíamos por la otra ecuación. Exacto. Y cómo esa propiedad, además, tiene aplicaciones superprácticas. Es la magia de las mates, ¿no? Una idea abstracta con consecuencias muy reales.
Pues resumiendo un poco. Hemos pasado de la ecuación $y = ax^2+bx+c$, entendiendo qué hace cada letra, a identificar puntos clave como el vértice y las raíces, y a entender la simetría.
Y finalmente, hemos llegado a la definición geométrica con el foco y la directriz, que explica propiedades como las de las antenas. Y todo esto, apoyándonos en las simulaciones para verlo en acción.
Y eso, creo, conecta directamente con la filosofía de AulaQuest, ¿verdad? Las matemáticas no son solo para memorizar fórmulas, sino para explorar, para tocar, para visualizar. Para entenderlas de forma interactiva.
Pues, oyentes, hemos hablado de trayectorias de objetos, de antenas, de faros... Pero ahora que se entiende un poco mejor qué es una parábola por dentro, esa relación foco-directriz, ¿dónde más creen que podría estar escondida esta curva?
¿En qué otros fenómenos naturales o tecnológicos podría estar jugando un papel secreto? Buena pregunta para cerrar. A observar el mundo con ojos parabólicos.

🔍 ¿Qué es una parábola?

La parábola es una de las figuras más fascinantes de la geometría. Forma parte del conjunto de las cónicas, junto a la elipse y la hipérbola. Se obtiene al cortar un cono con un plano paralelo a una de sus generatrices. Pero más allá de esa definición técnica, lo importante es que la parábola es una curva que aparece una y otra vez en física, ingeniería, y matemáticas: desde trayectorias de proyectiles hasta los reflectores parabólicos de antenas y focos.

Representación típica de las cónicas: circunferencia, elipse, parábola e hipérbola
Representación típica de las cónicas: circunferencia, elipse, parábola e hipérbola.

🧮 Ecuación general: la forma estándar

En Bachillerato trabajamos principalmente con esta forma:

$$ y = ax^2 + bx + c $$
  • a: determina la concavidad y la "apertura" de la parábola.
  • b: influye en el desplazamiento horizontal y la simetría.
  • c: indica dónde la parábola corta al eje Y.

🧪 Simulación 1: Explora los términos uno a uno

En esta primera simulación puedes mover los valores de a, b y c para ver el efecto de cada uno:

  • ax²: curva hacia arriba o hacia abajo según el signo de a.
  • bx: desplaza el eje de simetría.
  • c: sube o baja toda la parábola.

🎯 Vértice, raíces y eje de simetría

El vértice es el punto más alto o más bajo de la parábola. Se calcula con:

$$ x_v = \frac{-b}{2a}, \quad y_v = f(x_v) $$

Y si quieres encontrar los puntos donde la parábola corta al eje X, resuelves la ecuación cuadrática:

$$ ax^2 + bx + c = 0 $$

🧪 Simulación 2: Vértice, raíces y simetría

Aquí puedes visualizar:

  • El vértice con coordenadas en tiempo real.
  • Las raíces, si existen.
  • El eje de simetría marcado verticalmente.

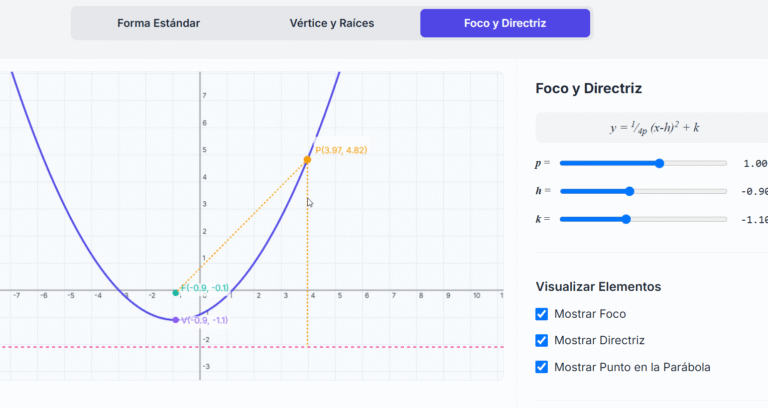
🔦 Foco y directriz: la definición geométrica

Una parábola es también el conjunto de puntos que están a igual distancia de un punto fijo (foco) y una recta fija (directriz).

La ecuación con vértice en \((h, k)\) es:

$$ y = \frac{1}{4p}(x - h)^2 + k $$
  • h: desplazamiento horizontal del vértice.
  • k: desplazamiento vertical.
  • p: distancia del vértice al foco y a la directriz.

🧪 Simulación 3: Foco y directriz en acción

  • Desliza los valores de p, h y k.
  • Observa cómo se sitúan el foco y la directriz.
  • Comprueba que todos los puntos están equidistantes al foco y a la directriz.

✅ Conclusión

Gracias a estas simulaciones, la parábola deja de ser solo una fórmula y se convierte en una experiencia que puedes ver, tocar y entender. En AulaQuest, la geometría se vive.

💥 ¿Listo para ver el mundo con ojos parabólicos? Elige tu Misión

Ya has explorado la parábola con deslizadores, has jugado con sus coeficientes y has visualizado cómo cambian el vértice, las raíces y el eje de simetría. Pero ahora llega el momento de ensuciarte las manos con la matemática de verdad.

Aquí tienes una propuesta de actividad de laboratorio dividida en distintos niveles y misiones. No es obligatorio completarlas todas: cada profesor puede decidir en qué retos centrarse según los objetivos del grupo, el tiempo disponible o el nivel del alumnado.

Es una experiencia abierta, flexible y pensada para adaptarse al aula real. Puedes hacerla en equipo, individualmente o como una investigación guiada. Lo importante no es llegar al final, sino explorar, formular conjeturas y ver cómo la parábola cobra vida en situaciones reales y visuales.

Bloque 1: Jugando con los Coeficientes (Simulación 1) 🎯

Este bloque se centra en entender el papel de cada letra en la ecuación $y = ax^2 + bx + c$. Usa la Simulación 1 para responder.

1.En la simulación, pon el coeficiente $a=2$ y luego cámbialo a $a=0.5$. ¿Qué le ha pasado a la forma de la parábola?



2. Si quieres mover la parábola verticalmente hacia arriba o hacia abajo, sin cambiar su forma ni su posición horizontal, ¿qué único coeficiente debes modificar?





3. Para entender bien cómo el coeficiente a controla la apertura (lo ancha o estrecha que es) de la parábola, vamos a usar una parábola de referencia: $y = x^2$.

Sigue estos pasos en la Simulación 1:

1. Primero, ajusta la parábola de referencia en el simulador con los valores: $a=1$, $b=0$ y $c=0$. Observa bien su forma y su apertura. Esta será tu base de comparación.

2. Ahora, sin modificar b y c (déjalos en 0), completa la siguiente tabla cambiando únicamente el valor de a. utiliza varios valores: positivos, negativos, grandes, pequeños…

Valor de aOrientación (hacia arriba / abajo)Comparada con $y=x^2$ (más ancha / más estrecha / igual)

4. El coeficiente $b$ es “más sutil”. Modifica únicamente el valor de $b$ en la simulación (por ejemplo, de -5 a 5).

Describe con tus palabras el movimiento que observas en el vértice de la parábola.
¿Es un simple desplazamiento horizontal?
¿Por qué crees que ocurre esto?



Bloque 2: Los Puntos Clave de la Parábola (Simulación 2) 🔬

Ahora nos centramos en el vértice, las raíces y el eje de simetría. Usa la Simulación 2, que te resalta estos elementos.

5. Dada la parábola $y = x^2 – 2x – 3$, ¿cuáles de las siguientes afirmaciones son ciertas?
(Puedes usar la simulación para comprobarlo).






6. Usa la fórmula $x = -\frac{b}{2a}$ para calcular la coordenada $x$ del vértice de la ecuación $y = -2x^2 – 8x – 6$.

Luego, introduce esa ecuación en la Simulación 2 y comprueba si tu cálculo coincide con el vértice que muestra el simulador.



7. Si en la simulación ajustas los parámetros para que la parábola no tenga ninguna raíz real (no corte el eje X), ¿dónde puede estar situado el vértice?







8. Explica la relación que existe entre el eje de simetría, el vértice y las raíces (cuando existen).

¿Cómo te ayuda la Simulación 2 a visualizar que las raíces están a la misma distancia del eje de simetría? Describe lo que ves.



Bloque 3: El Secreto Geométrico (Simulación 3) 📡

Este bloque explora la definición geométrica de la parábola a través del foco y la directriz. Usa la Simulación 3.

9. En la Simulación 3, ¿qué elemento geométrico determina hacia dónde se refleja una señal que llega paralela al eje de la parábola?



10.En la ecuación de la forma canónica $y = \frac{1}{4p}(x-h)^2 + k$, el valor de $p$ representa:






11. El foco y la directriz no son elementos decorativos; de hecho, son los que definen la forma exacta de cualquier parábola. Con este ejercicio, vas a descubrir la propiedad fundamental que conecta a cualquier punto de la curva con estos dos elementos.

Usa la Simulación 3 para realizar el siguiente experimento:

Procedimiento Experimental

1. En el simulador, establece valores para los parámetros $h$, $k$ y $p$ para dibujar una parábola.
2. Activa la opción que muestra el foco, la directriz y el puntop en la parábola.
3. Mueve el punto a tres posiciones diferentes a lo largo de la curva.
4. Para cada una de estas tres posiciones, anota las dos medidas que te proporciona la simulación:
– Distancia del punto al foco.
– Distancia del punto a la directriz.

Ahora, responde a lo siguiente basándote en los datos que has recogido:

Al comparar las dos distancias (al foco y a la directriz) en cada una de las posiciones, ¿qué relación matemática observas entre ellas? ¿Son una el doble que la otra, su suma es constante, o algo diferente?

Basado en tu descubrimiento, completa la siguiente frase que define la regla fundamental de toda parábola:

Una parábola es el conjunto de puntos del plano cuya distancia a un punto fijo llamado foco es siempre ____________ a su distancia a una recta fija llamada directriz.



Bloque 4: Conectando Ideas y Mirando el Mundo 🌍

Estas preguntas finales te invitan a sintetizar todo lo aprendido.

💡 Pregunta  para mentes parabólicas

Durante esta simulación has trabajado con dos formas muy potentes de la parábola: la forma estándar (la clásica ax² + bx + c) y la forma canónica con vértice, foco y directriz (esa del tipo (x – h)² y compañía).

Pero ojo: no son las únicas. Existen otras formas más generales, como la que aparece al estudiar cónicas en serio: algo así como Ax² + Bxy + Cy² + Dx + Ey + F = 0. No la hemos trabajado aquí, pero si algún día ves una parábola metida entre elipses e hipérbolas, ya sabes de dónde viene.

12. La pregunta es: ¿Cuándo te resulta más útil usar la forma estándar y cuándo prefieres la forma canónica? Piensa en qué tipo de información te da cada una más directamente: ¿el vértice?, ¿las raíces?, ¿la simetría?, ¿el foco?, ¿la dirección?

No hay una única respuesta correcta. Lo importante es que sepas elegir la herramienta adecuada según lo que quieras descubrir de la parábola.



La forma parabólica no solo existe en los libros de matemáticas; aparece constantemente en la naturaleza, la ingeniería y la tecnología. Los ejemplos más comunes son las antenas parabólicas (que concentran señales) y los faros de los coches (que proyectan la luz).

13. Piensa en otros ejemplos donde esta curva sea importante. Para cada uno, justifica tu elección basándote en una de las propiedades clave de la parábola:

  • Propiedad de reflexión: ¿La forma ayuda a concentrar o a proyectar energía (luz, sonido, calor) desde un punto focal?
  • Propiedad de trayectoria: ¿La forma describe el camino que sigue un objeto lanzado al aire bajo la influencia de la gravedad?
  • Propiedad estructural: ¿La forma ayuda a distribuir el peso o la tensión de manera eficiente, como en un puente o un arco?


📬 Instrucciones para enviar tus respuestas al profe

  1. Completa las actividades que te haya indicado tu profe.
  2. Haz clic en “Revisar y enviar al profe”.
  3. Revisa tus respuestas. Si necesitas corregir algo, pulsa “❌ Corregir”.
  4. Cuando estén bien, haz clic en “📋 Copiar respuestas”.
  5. Luego pulsa “📬 Abrir Gmail” y pega las respuestas en el correo.
  6. Escribe el asunto y el email del profe, y pulsa Enviar.

🛡️En AulaQuest no se guarda nada. Tus respuestas no se almacenan, no se asocian a tu cuenta y nadie más las verá. Es solo un canal directo y privado entre tú y tu profe.

📚 Zona Profe – Acceso exclusivo para docentes
Bienvenido a la Zona Profe. Aquí encontrarás las soluciones detalladas de las actividades propuestas para tus estudiantes. Cada una ha sido elaborada con rigor y cuidado, basándonos en los datos del simulador y principios físicos sólidos.

Eso sí, aunque revisamos todo con atención, puede colarse alguna imprecisión. Te recomendamos que, antes de usar estas soluciones para corregir o explicar en clase, verifiques los cálculos por si acaso. Gracias por tu confianza y por hacer de la ciencia algo emocionante.

🔒 Esta solución está disponible solo para docentes registrados.

¿Eres profe? Solicita acceso aquí para desbloquear los recursos exclusivos.

💥 ¿Has creado una actividad que ha hecho brillar los ojos de tus alumnos?

¿Un experimento que dejó a tu clase con la boca abierta?
¿Una forma única de explicar ese tema que siempre se atraganta?

🎓 No lo guardes solo para ti. Súbela, compártela, inspíranos.

En AulaQuest creemos que la educación se transforma compartiendo, no compitiendo.
Cada actividad que subes no es solo un recurso: es una chispa que puede encender la pasión por aprender en otra aula, en otro colegio, en otra parte del mundo.

💡 Si tu actividad nació a partir de una de nuestras simulaciones, cuéntalo.
🔥 Porque tu experiencia puede abrir caminos.
🌍 Y tu creatividad puede cruzar fronteras.

Simulaciones de Mate