Simulador de Gases ideales

🧪 Laboratorio de Gases Ideales Online

La simulación de gases ideales es una herramienta interactiva para experimentar con las leyes de Boyle, Charles y Gay-Lussac, observa cómo cambian presión, volumen y temperatura y analiza los resultados en tiempo real.

Si quieres saber más, visita nuestro Simulador de Cinética Molecular

  • 🔗 Categoría: Química | Termoquímica ↗️
  • 🎓 Nivel educativo: ESO
  • ⚙️ Dificultad: Media (4/10)
  • 📈 Visitas: 108
Nivel educativo ESO
Dificultad Media (4/10)
Visitas 108
Pantalla Completa
Pantalla Completa

Explorando el Mundo Invisible de los Gases Ideales

Hola, bienvenidos a una nueva exploración. Y hoy, bueno, un saludo muy muy especial a todos los estudiantes de Aula Quest que nos estáis escuchando. Hola a todos.
Sabemos que tenéis el simulador de gases ahí delante, ¿verdad? Pues sentíos libres, de verdad, tocad los controles, experimentad mientras charlamos. Sí, sí, esa es la idea, es la mejor forma de pillar esto.
Exacto. Es que así es como se aprende de verdad, tocando. Hoy nos metemos de lleno en ese mundo un poco invisible, pero superinteresante, de los gases ideales. Mmm. Y vamos a usar esta herramienta interactiva, pero no como una clase teórica, ¿eh?
Más bien como... como una ventana para ver cómo se mueven, cómo se comportan. Justo. El objetivo, a ver, es entender de forma intuitiva, casi jugando, qué pasa cuando cambiamos la presión $P$, el volumen $V$, la temperatura $T$...
...y la cantidad de gas, el número de partículas $N$. Eso. Queremos que esas leyes que suenan a veces un poco abstractas, ¿no? Boyle, Charles, Gay-Lussac, pues que cobren vida en la pantalla, que las veamos.
Exactamente. Es que estas leyes son fundamentales en física, en química, describen el comportamiento básico de los gases. Y lo bueno, lo potente de este simulador es precisamente eso, que convierte las ecuaciones, que a veces asustan un poco, en algo visual.
Claro. Puedes casi espiar a las partículas, ver qué hacen y cómo eso a gran escala da lugar a la presión o la temperatura que medimos. Pasamos de lo micro a lo macro. Genial, suena muy bien.
Pues vamos al lío. Empecemos por el principio. ¿Cuáles son esas... esas piezas clave, esas variables que definen cómo está un gas?

Las 4 Variables Fundamentales de los Gases

Son cuatro las fundamentales. La primera, la presión, la $P$. Que no es algo raro, ¿eh? Es simplemente el resultado de que las partículas del gas están todo el rato chocando contra las paredes del recipiente. Ah, vale.
Imagínate millones y millones de golpecitos pequeñitos cada segundo. Pues eso, acumulado, es la presión. La medimos en atmósferas o en pascales. Bueno. Entendido, golpes.
Luego está el volumen, la $V$. Es el espacio, ¿no? El sitio que ocupa el gas dentro del cacharro este, del contenedor. El tamaño de la caja, digamos. Eso es. El campo de juego donde se mueven las partículas. Se mide en litros, metros cúbicos...
Vale. La tercera es la temperatura, $T$. Y ojo, ¿eh?, que esto es importante. No es solo si hace frío o calor. Ajá. Físicamente, es una medida de la energía cinética media de las partículas.
O sea, nos dice, en promedio, cómo de rápido se están moviendo. Ah, la agitación, ¿no? Exacto. La agitación molecular. Y muy importante, en ciencia usamos la escala Kelvin ($K$), la escala absoluta.
El cero Kelvin es donde en teoría no habría movimiento. Vale, Kelvin, no Celsius. Anotado. La cuarta variable es el número de partículas, $N$. Esta es fácil, simplemente cuántas bolitas de gas, átomos o moléculas, tenemos ahí metidas.
El número de jugadores. Justo. Cuantas más partículas, más jugadores en el campo. Perfecto. $P$ por choques, $V$ el espacio, $T$ la velocidad media en Kelvin, y $N$ la cantidad.

Partículas Ligeras vs. Pesadas

Y has hablado de partículas. Veo que en el simulador hay como dos colores, ¿no? ¿Azules y rojas? Correcto. Es una forma muy visual de representar el efecto de la masa de las partículas, la masa molar.
Las partículas ligeras, las azules, pues representan gases ligeritos como el helio, el hidrógeno. Tienen poca masa. Vale. Y las partículas pesadas, las rojas, simulan gases con más masa, pues como el argón o el dióxido de carbono.
Y la diferencia principal es, ¿cómo se mueven o...? Exacto. Ahí está la clave. A una misma temperatura... recuerda, la $T$ mide la energía cinética media... Sí. Pues para tener la misma energía media, las partículas que pesan menos, las azules, tienen que moverse de media más rápido que las rojas, las pesadas.
Ah, claro. Son más ágiles. Eso. Son más ágiles. Lo podéis ver perfectamente en el simulador si metéis de los dos tipos y subís la temperatura. Las azules van como locas comparadas con las rojas. Qué bueno.
Ya. Ya empezamos a ver conexiones. Y si ahora, por ejemplo, dejo el volumen quieto y la temperatura quieta y le doy a la bomba para meter más partículas, anda, la presión sube.
Claro. Tiene sentido, ¿no? Si hay más partículas, pues chocarán más veces contra las paredes. Precisamente. Has aumentado $N$ manteniendo $V$ y $T$ constantes. Y el resultado directo es que $P$ aumenta. Es la primera intuición, muy buena, de cómo se conectan las variables.

El Papel del Calor y el Frío

Vale, vale. Ahora si te parece profundizamos un poco en la temperatura. Esos controles de la llama, fuego, y el cubito de hielo son super importantes. Sí, ¿qué hacen exactamente?
Pues mira, cuando añades calor, lo que estás haciendo es meter energía en el sistema, en el gas. Mmm. Las partículas absorben esa energía, su energía cinética aumenta y por lo tanto se mueven más rápido.
Fijaos en el simulador, se ve genial cómo aumenta la agitación, parece que se vuelven más frenéticas. Sí se ve, se ve. Y al revés, si añades frío, estás quitando energía. Las partículas pierden energía cinética, van más lentas.
Se calman. Eso es, se calman. El movimiento es más pausado, prácticamente puedes ver cómo se ralentizan. Vale. Y una cosilla sobre la temperatura mínima, el cero absoluto, 0 Kelvin, que son como -273 grados Celsius, ¿vale?
Sí. Es el punto teórico donde se pararía todo movimiento molecular. Pero es teórico, es un límite al que no podemos llegar en la práctica por cosas de cuántica y termodinámica. Por eso el simulador tiene un mínimo de 1 K, no llega al cero absoluto.
Entendido. Un límite físico real. Vale, pues ya tenemos los ingredientes. $P$, $V$, $T$, $N$, partículas rápidas, lentas... Ahora viene lo bueno, ¿no? Usar el simulador para comprobar esas leyes famosas.

La Ley de Boyle: Relación Presión-Volumen (Temperatura Constante)

Vamos a ello. Venga, estudiantes de Aula Quest, preparad los controles. Empecemos por... la ley de Boyle. ¿Qué pasa si cambiamos el volumen pero... pero mantenemos la temperatura constante? A ver.
La ley de Boyle describe un proceso isotérmico, o sea, a temperatura constante. Y lo que dice es algo muy elegante: a $T$ constante, la presión y el volumen de una cantidad fija de gas son inversamente proporcionales.
¿Inversamente? O sea... que si uno sube, el otro baja y viceversa. Si comprimes el gas a la mitad de su volumen inicial, su presión se duplica. Si lo expandes al doble, la presión baja a la mitad. La fórmula es: $$ P \cdot V = \text{constante} $$ O también: $$ P_1 V_1 = P_2 V_2 $$
Ah, vale. Vamos a verlo. En el simulador hay que seleccionar la opción para mantener la $T$ constante. Suele poner Ley de Boyle o algo así. Sí, busca $T$ constante o isotérmico. Vale.
Ahora meto unas 50 partículas, da igual azules o rojas por ahora, ¿no? Sí, para esto da igual. Anota la presión y el volumen que marca al principio. Hecho. Y ahora uso la pared esa que se mueve, la lateral, y reduzco el volumen justo a la mitad. A ver qué dice el manómetro.
¡Ostras! ¿Qué ha pasado? Se ha duplicado. Prácticamente el doble de presión que antes. ¡Qué bueno! ¿Ves? Funciona. Puede haber alguna pequeña fluctuación, es estadística, pero debería estar muy cerca del doble.
Clavado. Y... ah, si activo el contador de colisiones... se dispara. Ahora marca muchos más choques por segundo. Claro, tiene todo el sentido. Son las mismas partículas con la misma energía media, porque $T$ es constante, pero ahora tienen la mitad de espacio.
Chocan el doble de veces. Exacto. Chocan contra las paredes con el doble de frecuencia y eso es literalmente la presión. ¡Qué visual es! La relación $P \propto 1/V$ no es magia, es por el espacio.
Me encanta verlo así. Y si quieres ir un paso más allá, puedes usar la herramienta de registro de datos ya mismo. Guardas el estado inicial ($P_1, V_1$), guardas este estado final ($P_2, V_2$). Ah, buena idea.
Y luego puedes hasta exportar esos datos a un CSV y comprobarlo con números en una hoja de cálculo.

La Ley de Gay-Lussac: Relación Presión-Temperatura (Volumen Constante)

Genial, integrando las herramientas. Vale, perfecto Boyle. Siguiente caso. ¿Y si ahora la caja es rígida? O sea, el volumen no puede cambiar, pero le metemos calor. Eso es, Gay-Lussac.
Correcto. La ley de Gay-Lussac. Es un proceso a volumen constante, que se llama isocórico. Isocórico, vale. Y lo que dice es que la presión de una cantidad fija de gas es directamente proporcional a su temperatura absoluta, en Kelvin, claro.
O sea, que si una sube, la otra también. Eso es. Si calientas el gas, sus partículas se mueven más rápido. Como el volumen es fijo, no tienen más sitio, así que chocarán contra las paredes más a menudo y con más fuerza.
Y eso hace que suba la presión. Exacto. Más frecuencia y más fuerza en los choques, igual a más presión. La fórmula es: $$ \frac{P_1}{T_1} = \frac{P_2}{T_2} $$
A comprobarlo. Selecciono volumen constante, ley de Gay-Lussac, meto bastantes partículas ahora, ¿no?, para que se note bien. Unas 100-150. Sí, mejor bastantes, así el efecto es más claro.
Vale. Y ahora, le doy al calor, subo la $T$ poco a poco y miro el termómetro en Kelvin y el manómetro. Anda, ¿qué observas? Pues que la presión sube, y parece que sube de forma bastante lineal con la temperatura en Kelvin. Sube y sube.
Las partículas van como locas ahí dentro. Es una relación directa clarísima. Más $T$, más agitación, más $P$. Pero, ojo, que si sigo calentando... ¡Ostras! ¡Pum! Me acaba de salir un aviso.
El contenedor ha explotado. Presión: 50 atmósferas. Ajá. Esa explosión virtual es una lección super importante. ¿Por qué? Porque eso es exactamente lo que puede pasar en la vida real si calientas demasiado algo cerrado y rígido que contiene gas.
Una lata de aerosol, una olla a presión olvidada en el fuego. Claro, la presión aumenta con la temperatura sin parar, porque el volumen no puede ceder, hasta que el material del recipiente dice "basta" y ¡pum!, explota.
Es Gay-Lussac llevado al extremo, y puede ser peligroso de verdad. Uf, qué conexión más directa. Vale, muy claro.

La Ley de Charles: Relación Volumen-Temperatura (Presión Constante)

Nos queda una combinación, creo. ¿Qué pasa si dejamos que el volumen cambie, que la caja se pueda expandir o contraer, para que la presión se mantenga constante mientras calentamos?
Esa es la ley de Charles. Un proceso a presión constante, que se llama isobárico. Isobárico, okay. Y dice que, a presión constante, el volumen de una cantidad fija de gas es directamente proporcional a su temperatura absoluta en Kelvin.
Otra vez directa. Si sube $T$, sube $V$. Exacto. Si calientas un gas y le permites expandirse, como en un globo que no está lleno del todo, o en un cilindro con un pistón que se pueda mover libremente, ocupará más espacio.
Necesita más volumen para mantener la presión igual. La fórmula es: $$ \frac{V_1}{T_1} = \frac{V_2}{T_2} $$
¿Y cómo se ve eso en el simulador? A ver... Tienes que seleccionar la opción de presión constante, Ley de Charles, y asegurarte de que la temperatura pueda variar. Mete partículas como antes.
Vale. Presión constante, $T$ variable. Añado partículas... listo. Y ahora, le doy calor... ¡Ah, mira! La pared de la derecha se está moviendo hacia fuera.
¿Lo ves? Sí, el volumen está aumentando según sube la temperatura. ¿Por qué hace eso? Pues para mantener la presión constante, que es la condición que hemos fijado. Al calentar, las partículas van más rápido, chocarían más fuerte y más a menudo, ¿verdad?
Sí, como en Gay-Lussac. Tendería a subir la presión. Exacto. Pero como aquí queremos que la $P$ se mantenga fija, el sistema lo que hace es dejar que el volumen aumente. Al tener más espacio, las partículas tardan un poquito más en ir de pared a pared, así que la frecuencia de los choques disminuye un poco.
Ah. Y esa menor frecuencia compensa la mayor fuerza de cada choque. El resultado neto es que la presión se quede igual. ¡Qué ingenioso! Se autoajusta. Es el principio básico de los globos aerostáticos.
Calientas el aire dentro, se expande (aumenta $V$), se vuelve menos denso que el aire de fuera y... ¡para arriba! Es Charles en acción.

Conectando el Mundo Micro y Macro

Fascinante. Oye, pues hemos visto las tres leyes principales funcionar. Y antes mencionaste el registro de datos y el contador de colisiones. ¿Hay alguna otra herramienta en el simulador que sea útil para para investigar más?
Sí, aparte del registro de datos, que como decíamos, es genial porque puedes exportar a CSV y analizar números de verdad... Sí, eso es un puntazo para hacer gráficas y tal. Exacto.
Aparte de eso, está la opción de medidas del recipiente, que te da el ancho exacto del contenedor en nanómetros en tiempo real. ¿Y eso para qué sirve? Pues es super útil para comprobar la ley de Boyle de forma cuantitativa.
Como la presión es inversamente proporcional al volumen, y el volumen aquí depende directamente del ancho (si la altura y profundidad son fijas), pues puedes ver si $P$ es inversamente proporcional al ancho. Mides el ancho inicial, el final, y ves si la presión cambió justo al revés.
Ah, muy bueno. Para ser más preciso. Vale. Oye, pues todas estas leyes, estas observaciones nos llevan siempre a lo mismo, ¿no? A esa conexión entre lo que hacen las partículas pequeñitas y lo que medimos a lo grande.
Exactamente. Ese es el mensaje clave, creo yo. Lo que sentimos o medimos como temperatura en nuestro mundo macroscópico no es más que el reflejo de la energía cinética media de esas billones de partículas invisibles. La agitación, la velocidad media a la que se mueven.
La $T$ es movimiento. Y lo que medimos como presión es el resultado global, el efecto acumulado de los incesantes bombardeos de esas partículas contra las paredes, la frecuencia con la que chocan y la fuerza con la que lo hacen.
La $P$ son los choques. Si repasamos Gay-Lussac otra vez, la cadena causa-efecto es súper clara. Doy calor, aumento $T$, las partículas van más rápido, aumenta su energía cinética media, chocan más veces y más fuerte contra las paredes, que están fijas, mido más presión. La presión es la manifestación externa de toda esa energía y movimiento interno.

Resumen y un Reto Final

Queda clarísimo viéndolo así. Entonces, resumiendo un poco, ¿qué nos llevamos de todo esto? Hemos visto las cuatro variables clave: $P, V, T, N$. Hemos jugado con las tres leyes fundamentales: Boyle, Charles, Gay-Lussac.
Viendo cómo se relacionan entre sí y hemos descubierto herramientas para medir y analizarlo todo. Para mí, lo más potente es eso, ver tan claro cómo ese caos aparente de millones de bolitas moviéndose... Ajá. ...da lugar a leyes físicas súper predecibles que explican cosas de todos los días, como hinchar una rueda o por qué explota un spray al sol.
Es esa conexión entre lo invisible y lo que vemos y medimos. Totalmente de acuerdo. Y, bueno, para dejar una idea ahí flotando, algo para darle una vuelta y quizás seguir jugando con el simulador... Venga.
Hemos visto partículas ligeras (las azules), que van rápido, y pesadas (las rojas), que van más lentas a la misma $T$. Ahora imagina que metemos una mezcla de las dos en la caja. Mantenemos $V$ y $T$ constantes.
¿Cómo crees que afectará esa mezcla a la presión total, comparado con si solo hubiera un tipo de gas? Uy, buena pregunta. ¿Será la presión simplemente la suma de las presiones que haría cada gas por separado si estuviera solo?
Eso es lo que dice la ley de Dalton de las presiones parciales. ¿O hay alguna... alguna sutileza en cómo esas partículas de distinta masa y velocidad comparten la energía total y contribuyen a los choques?
Interesante. Cómo interactúan al mezclarse. Exacto. Es un pasito más allá de las leyes básicas que hemos visto hoy. Ahí lo dejo. Pues una excelente pregunta para seguir indagando.
Animamos a todos los estudiantes de Aula Quest a que sigáis jugando con el simulador. Probad esa mezcla, cambiad los parámetros a lo loco, a ver qué pasa si abrís la tapa. Sed curiosos, experimentar es la mejor forma de que todo esto se quede grabado.
Sin duda. Pues hasta aquí nuestra inmersión de hoy en el fascinante mundo de los gases. Gracias por acompañarnos. Gracias a vosotros. ¡A experimentar!

🔬 Guía para el Simulador de Gases Ideales: ¿Qué voy a aprender?

¡Bienvenido a tu laboratorio de gases ideales virtual! Este simulador interactivo es una herramienta educativa diseñada para explorar el comportamiento de los gases a nivel molecular. Aprenderás de forma práctica la relación fundamental entre cuatro variables clave de la termodinámica:

  • Presión (P): La fuerza por unidad de área que ejercen las partículas al chocar incesantemente con las paredes del recipiente.
  • Volumen (V): El espacio tridimensional que ocupa el gas, definido por los límites del contenedor.
  • Temperatura (T): Una medida directa de la energía cinética media y, por tanto, de la velocidad promedio de las partículas.
  • Número de Partículas (N): La cantidad de materia gaseosa (átomos o moléculas) presente en el sistema.

El objetivo de este experimento virtual de gases es que interactúes con estos parámetros para comprender a fondo las famosas Leyes de los Gases (Boyle, Charles, Gay-Lussac) de una manera visual e intuitiva.

💨 Partículas, Temperatura y Energía Cinética en el Simulador de Gases

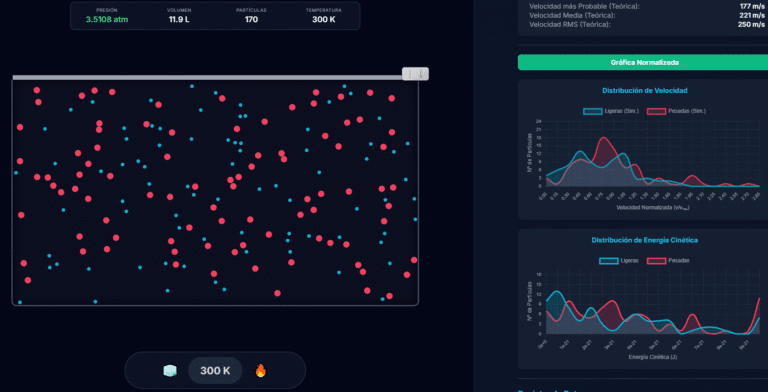
Dentro de este laboratorio de gases, puedes inyectar dos tipos de partículas para simular diferentes sustancias gaseosas:

  • 🔵 Partículas Ligeras (azules): Representan gases de baja masa molar. A la misma temperatura, se mueven mucho más rápido.
  • 🔴 Partículas Pesadas (rojas): Simulan gases más masivos. A la misma temperatura, su velocidad media es menor.

Referencia al Simulador: Usa los botones del panel lateral para añadir partículas. Observa cómo la presión aumenta al añadir más gas, incluso si no cambias ni el volumen ni la temperatura.

Temperatura: La Energía del Movimiento

La temperatura (medida en Kelvin, la escala absoluta) es una medida directa de la energía cinética media de las partículas. A más temperatura, mayor agitación térmica, lo que significa que se mueven más rápido y chocan con más fuerza y frecuencia.

  • 🔥 Añadir Calor: Transfiere energía al sistema, aumentando la velocidad de las partículas.
  • 🧊 Añadir Frío: Retira energía del sistema, disminuyendo la velocidad de las partículas.

Referencia al Simulador: Usa los controles de calor/frío y fíjate en cómo el movimiento de las partículas cambia instantáneamente. Al calentarlas, se agitan frenéticamente; al enfriarlas, se vuelven más lentas.

¿Por qué no se puede llegar a 0 Kelvin?

El simulador te permite llegar hasta 1 K, pero no a 0 K. El Cero Absoluto (0 K) es la temperatura teórica a la que cesaría todo movimiento molecular. Es un concepto límite fundamental en la física y la termodinámica, inalcanzable en la práctica pero crucial para entender la teoría.

📜 Ley de Boyle: ¿Qué pasa con la presión y el volumen a temperatura constante?

La Ley de Boyle, uno de los pilares del estudio de los gases, describe cómo a temperatura constante (un proceso isotérmico), la presión que ejerce un gas es inversamente proporcional a su volumen. En palabras sencillas: si comprimes el gas a la mitad de su volumen, su presión se duplica.

$ P_1 V_1 = P_2 V_2 $

🧪 Experimento Virtual de la Ley de Boyle

  1. En el panel lateral, selecciona "Ley de Boyle" para mantener la temperatura fija.
  2. Añade unas 50 partículas (ligeras o pesadas). Anota la presión y el volumen iniciales.
  3. Usa el deslizador lateral para reducir el volumen del recipiente a la mitad.
  4. Observa el manómetro y el contador de colisiones: ¿Qué ha pasado con la presión? ¡Debería haberse duplicado! Esto demuestra visualmente que al tener menos espacio, las partículas chocan mucho más a menudo contra las paredes.

🔥 Ley de Gay-Lussac: La relación entre Presión y Temperatura a Volumen Constante

Esta ley, fundamental en termodinámica, explica qué ocurre en un recipiente rígido (volumen constante, un proceso isocórico). La presión del gas es directamente proporcional a su temperatura absoluta (medida en Kelvin).

$ \frac{P_1}{T_1} = \frac{P_2}{T_2} $

💥 Simulación de la Ley de Gay-Lussac

  1. Selecciona "Ley de Gay-Lussac". El volumen del recipiente quedará fijo.
  2. Añade un buen número de partículas (unas 100-150) para que el efecto sea claro.
  3. Usa el control de 🔥 para aumentar la temperatura gradualmente.
  4. Observa la relación directa: A medida que sube la temperatura, la presión aumenta linealmente. Las partículas, más energéticas, golpean las paredes con más fuerza y frecuencia.
  5. ¡Cuidado! Si la presión supera las 50 atm, el recipiente explotará. ¡Esta es una simulación segura de lo que le ocurre a un aerosol si lo arrojas al fuego, un ejemplo práctico de la Ley de Gay-Lussac!

🎈 Ley de Charles: ¿Cómo se relacionan Volumen y Temperatura a Presión Constante?

La Ley de Charles explica por qué los globos aerostáticos se elevan. A presión constante (un proceso isobárico), el volumen que ocupa un gas es directamente proporcional a su temperatura absoluta. Si calientas un gas, necesita expandirse para que su presión no aumente.

$ \frac{V_1}{T_1} = \frac{V_2}{T_2} $

🎈 Experimento Interactivo de la Ley de Charles

  1. Elige "Ley de Charles". Verás que la presión se mantiene constante.
  2. Selecciona la sub-opción "Variar Temperatura".
  3. Añade partículas y luego usa el control de 🔥 para calentar el gas.
  4. Observa la expansión: Verás cómo el volumen del recipiente aumenta automáticamente. La pared lateral se desplaza para dar más espacio a las partículas agitadas y así mantener la presión constante, tal como ocurriría en un recipiente con un pistón móvil.

📈 Herramientas del Laboratorio Virtual: Análisis de Datos y Mediciones

Este simulador de gases ideales va más allá de la simple visualización; es un completo cuaderno de laboratorio digital. Aprende a usar sus herramientas para tomar medidas precisas, realizar análisis de datos y preparar informes o proyectos de física y química.

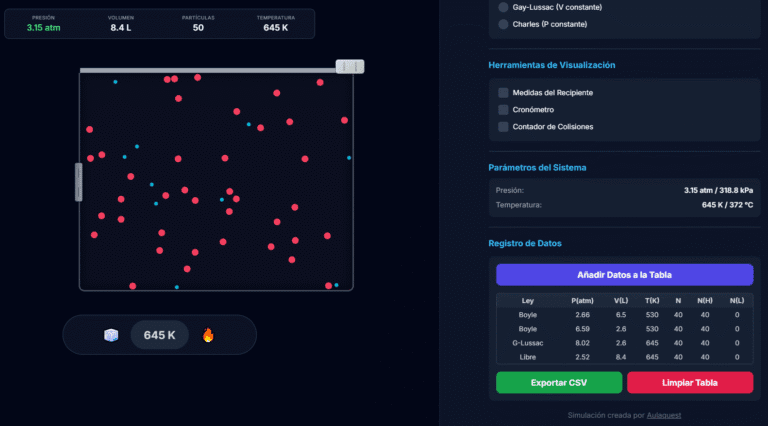
Registro de Datos: Tu Cuaderno Digital

Esta es la herramienta más potente para el análisis cuantitativo. Te permite guardar una "foto" del estado del sistema en cualquier momento.

  • ¿Cómo se usa?: Realiza un experimento. Antes de cambiar un parámetro, pulsa "Añadir Datos a la Tabla". Luego, haz el cambio, espera a que el sistema se estabilice y vuelve a pulsar para registrar el nuevo estado.
  • ¿Qué guarda?: Cada fila es una instantánea con P, V, T, y el número de partículas totales (N), pesadas (N(H)) y ligeras (N(L)).
  • Exportar a CSV: ¡Esta es la funcionalidad clave para un análisis científico! Al terminar, pulsa "Exportar CSV" para descargar todos los datos. Podrás importarlos en Excel, Google Sheets o Python para crear gráficas profesionales, calcular constantes y verificar las leyes de los gases matemáticamente.

Otras Herramientas

  • Contador de Colisiones: Actívalo para medir la frecuencia de choques contra las paredes. Es la prueba visual de que la presión, a nivel microscópico, es el resultado de un bombardeo incesante de partículas.
  • Medidas del Recipiente: Muestra el ancho exacto del contenedor, útil para verificar cuantitativamente la relación inversa en la Ley de Boyle ($P \propto 1/V$).

Zona de Actividades de tu Profesor

Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.

¿Tu última clase con la simulación fue un éxito?

Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Crear una actividad es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.

  • 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
  • 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
  • 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
📤 Subir mi actividad

*Esto es solo para profes. Si lo eres, pide tu acceso.

Simulaciones en Química

No necesitas dar la clase perfecta

Solo necesitas que tus alumnos entiendan. Usa nuestras simulaciones y cambia el chip sin perder tiempo ni energía.

Zona Profe
Comparte con tus compañeros de clase