Simulador Masa-Resorte

🧪 Simulador Interactivo Masa - Resorte Ley de Hooke

La Ley de Hooke describe cómo se comportan los sistemas elásticos cuando se les aplica una fuerza. Este simulador interactivo de muelles te permite estudiar la relación entre la deformación de un resorte y la fuerza que actúa sobre él.

Este simulador de resortes verticales te permite colgar masas, ajustar la constante del resorte y controlar la amortiguación. Elige el planeta en el que quieres experimentar o compara el comportamiento de dos muelles distintos.
Una herramienta visual, precisa y rigurosa para enseñar lo invisible: las leyes que gobiernan el comportamiento elástico.
Nivel educativo ESO
Dificultad Media (4/10)
Visitas 80

📋 Detalles de la simulación

  • 🔗 Categoría: FÍSICA | Dinámica↗️
  • 🎓 Nivel educativo: ESO
  • ⚙️ Dificultad: Media (4/10)
  • 📈 Visitas: 80

¿Qué te ha parecido la simulación?

★★★★★
5,0 de 5 (2 valoraciones)

Oscilaciones y Energía: Explorando Sistema Masa-Resorte

Hola. Para quienes estáis en Aula Quest ahora mismo, eh, veréis que tenéis delante una simulación interactiva genial. Vamos a usarla juntos, ¿vale?, para meternos de lleno en el mundo de los muelles y, bueno, y cómo oscilan las cosas.
Exacto, como tener un pequeño laboratorio ahí mismo, en la pantalla.
Eso es. Mirad la pantalla. A la izquierda está el lienzo, donde, donde colgamos los muelles y las masas. Y a la derecha el panel de control. Podemos empezar con calma, en modo un muelle, para pillar lo básico.
O si no, ir directos a dos muelles para comparar, como en un experimento de verdad.
Sí, y los controles clave. A ver, tenemos la masa ($m$), la constante del muelle ($k$), que esto indica si es más blando o más duro, ¿no?
Justo. Una $k$ alta es un muelle duro, una $k$ baja, uno blando.
Luego el planeta, para cambiar la gravedad ($g$), podemos ir a la Luna o a Júpiter. Y el amortiguamiento, que es como la fricción, ¿verdad?
Eso es. Si pones amortiguamiento cero, el sistema es ideal, no pierde energía. Si lo aumentas, pues el movimiento se va frenando.
Vale. ¿Listo para ver qué pasa al colgar una masa? ¿Qué fuerzas entran en juego?
Claro. Al colgar la masa, lo primero, su peso. La fuerza de la gravedad ($F_g = mg$). Siempre tira hacia abajo.
Es el vector rojo que vemos en la simulación, ¿no?
El mismo. Y oponiéndose a él está la fuerza elástica del muelle. Esta sigue la famosa ley de Hook: $$ F_e = -kx $$ Es el vector verde.
Ajá. Y ojo con ese signo negativo, que es, eh, crucial.
¿Por qué es tan importante?
Porque significa que la fuerza siempre intenta devolver el muelle a su posición original, sin estirar. Se opone al desplazamiento ($x$). Si estiras hacia abajo, la fuerza tira hacia arriba.
Entiendo. Es una fuerza restauradora.
Justo, esa es la palabra. Y cuando la masa se queda quieta, colgada, es porque está en equilibrio.
El punto donde las dos fuerzas se anulan.
Exactamente. El peso hacia abajo ($mg$) y la fuerza elástica hacia arriba ($kx$) son iguales en magnitud. Es esa línea discontinua verde que marca la simulación.
Vale, equilibrio entendido. Pero lo interesante es cuando se mueve, ¿no? Ese vaivén, la oscilación. ¿Cómo empieza eso?
Buena pregunta. Pues simplemente sacando la masa de ese punto de equilibrio. Imagina que la estiras un poquito más hacia abajo... y la sueltas.
¡Ah!
Al soltarla, la fuerza elástica hacia arriba es mayor que el peso hacia abajo, así que la masa acelera hacia arriba. Pasa por el punto de equilibrio a toda velocidad.
Toda velocidad, sí. Sigue subiendo, comprime el muelle. Ahí la fuerza elástica empuja hacia abajo, sumándose al peso. Frena, se para un instante arriba... y vuelta a empezar hacia abajo.
Exacto. Ese ciclo continuo es lo que llamamos movimiento armónico simple, o MAS para abreviar.
Y vemos en la simu los vectores de velocidad ($v$) en azul y aceleración ($a$) en amarillo, que cambian todo el rato. ¿Cómo, cómo se relacionan?
Pues fíjate bien. La velocidad es máxima justo cuando pasa por el punto de equilibrio. Ahí va lo más rápido posible.
Y cero en los extremos. Lógico, porque se para para cambiar de dirección.
Eso es. Y la aceleración es justo al revés. Es máxima en los extremos, porque ahí la fuerza neta, la suma de peso y elástica, es mayor.
Y cero en el centro, en el punto de equilibrio.
Correcto. Porque ahí las fuerzas se compensaban momentáneamente, si estuviéramos en reposo. Aunque aquí está pasando a toda velocidad, la fuerza neta es cero en ese instante.
Entendido. Oye, y debajo de todo, está la gráfica de energías. Veo barras de colores: cinética, potencial elástica, potencial gravitatoria. ¿Qué nos cuenta eso?
Esa gráfica es, eh, fascinante. Te muestra cómo se va transformando la energía en el sistema. La cinética es la energía del movimiento, depende de la velocidad.
Vale. Más velocidad, más energía cinética.
Exacto. Luego está la potencial elástica ($E_{pe}$), que es la energía que almacena el muelle al deformarse, al estirarse o comprimirse. Depende de $x$ y de $k$.
Y la potencial gravitatoria ($E_{pg}$), que depende de la altura ($h$) de la masa.
Correcto. $mgh$.
Y veo que hay una barra de energía total. Si quito el amortiguamiento... ah, a ver... ahora. Se queda fija.
Exacto. Eso es súper importante. Es la conservación de la energía mecánica. Si no hay fricción, o sea, amortiguamiento cero, la energía mecánica total (la suma de cinética y las dos potenciales) no cambia.
Solo se transforma de un tipo a otro.
Justo. La energía va pasando de cinética a potencial elástica, a potencial gravitatoria, y vuelta a empezar. Es como si cambiara de forma, pero la cantidad total es siempre la misma.
Qué bueno. Pero, ¿y si añado amortiguamiento? A ver, un poquito.
¿Ves? Ahora la barra de energía total empieza a bajar. Y aparece una barra de energía térmica que sube.
Claro. El amortiguamiento simula la fricción, el rozamiento. Esa fricción hace que la energía mecánica se "pierda". Pero en realidad no se pierde, se transforma en calor, energía térmica.
Por eso en el mundo real las cosas que oscilan acaban parándose.
Exactamente. La energía se disipa en forma de calor hacia el entorno.
Genial. Pues con todo esto mucho más claro, ahora volver al modo "dos muelles" tiene, tiene mucho más sentido para comparar.
Sí, es ideal para hacer experimentos controlados. Puedes probar, por ejemplo, misma masa, pero dos muelles con diferente $k$.
Veremos que el muelle más duro, el de mayor $k$, oscila más rápido.
Seguro. O al revés: mismo muelle, pero masas diferentes.
La masa más grande oscilará más despacio.
Eso es. O incluso comparar sistemas idénticos en planetas distintos. Poner uno en la Tierra y otro en la Luna, por ejemplo.
Para ver el efecto puro de la gravedad ($g$) en el periodo.
Y se pueden usar la regla y el cronómetro que trae la simulación para medir cosas, ¿no?
Claro, para medir la amplitud, el periodo... es hacer ciencia de verdad, pero de forma virtual.
Pues sí. Hemos ido desde simplemente colgar una masa hasta entender la ley de Hook, el vaivén del MAS, y cómo la energía se transforma y se conserva... o se disipa. Y todo, ¿eh?, jugando con la simulación.
Esa es la gran ventaja de estas herramientas interactivas. Te permiten ver, tocar casi, conceptos de física que a veces son un poco abstractos. Los hacen mucho más tangibles.
Totalmente de acuerdo. Y bueno, como reflexión final para todos, hemos visto muy claro cómo la energía cambia de forma aquí, en este sistema de muelle-masa. Quizás podríamos pensar ahora dónde más en nuestro día a día vemos estas transformaciones de energía. A lo mejor de formas que no son tan obvias como un muelle que sube y baja.

¿Qué es la "Constante del Muelle (k)" y cómo afecta al movimiento?

La constante del muelle, representada como $k$, es una medida de su dureza o rigidez. Se mide en Newtons por metro (N/m). Entender este concepto es clave para dominar cualquier simulador masa-resorte.

  • Un valor de $k$ bajo corresponde a un muelle "blando", fácil de estirar.
  • Un valor de $k$ alto corresponde a un muelle "duro", que requiere mucha fuerza para deformarse.
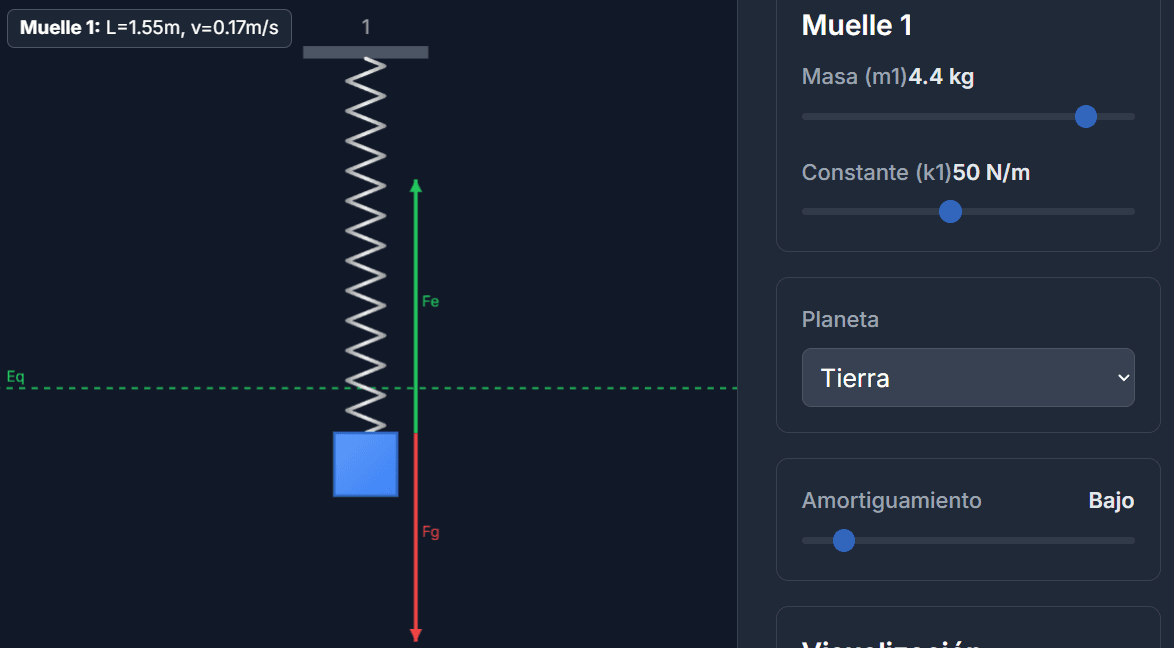
sistema masa-resorte.
Imagend e una masa oscilando en el simulador masa-resorte. La constante K es la que controla la rigidez del muelle.

En la simulación, al aumentar $k$, verás que para la misma masa, el muelle se estira menos y oscila mucho más rápido. ¡Prueba a compararlo usando el modo "Dos Muelles" con diferentes valores de $k$!

¿Por qué puedo cambiar de planeta? ¿Qué efecto tiene la gravedad ($g$)?

Cambiar de planeta te permite modificar la aceleración de la gravedad ($g$), que es la intensidad con la que el planeta atrae a la masa. La fuerza de la gravedad, también llamada Peso, se calcula como:

$$ F_g = m \cdot g $$

Donde $m$ es la masa. Al ir a la Luna, $g$ es mucho menor, por lo que el peso disminuye y el muelle se estira menos. En Júpiter, con su enorme gravedad, el peso es mucho mayor.

En la simulación: Observa cómo la posición de equilibrio (línea discontinua verde) cambia drásticamente al seleccionar diferentes planetas. Esto afecta a la energía potencial gravitatoria del sistema.

¿Qué es la Ley de Hooke y por qué la fórmula tiene un signo negativo?

La Ley de Hooke describe la fuerza que ejerce un muelle cuando se deforma. La fórmula es la estrella de esta simulación:

$$ F_e = -k \cdot x $$

Aquí, $k$ es la constante del muelle y $x$ es el desplazamiento desde su longitud natural. El signo negativo es crucial: indica que la fuerza del muelle es una fuerza restauradora. Siempre se opone al desplazamiento para intentar devolver al muelle a su estado original.

En la simulación: Activa los "Vectores de Fuerza". La fuerza elástica (vector verde) siempre apunta hacia la posición de equilibrio, oponiéndose al estiramiento o compresión.

¿Qué es la "posición de equilibrio" y por qué es importante?

La posición de equilibrio es el punto donde la masa se quedaría quieta. En este punto, la fuerza de la gravedad (peso) y la fuerza elástica se anulan mutuamente:

$$ F_e = F_g \implies k \cdot x_{eq} = m \cdot g $$

Esta posición es el centro del movimiento oscilatorio. Cuando la masa oscila, se mueve simétricamente alrededor de este punto, que es donde su velocidad es máxima y su aceleración es cero.

En la simulación: La posición de equilibrio está marcada con una línea discontinua verde. Úsala como referencia para entender el movimiento.

¿Cómo funciona la conservación de la energía en este sistema masa-resorte?

Si no hay fricción (amortiguamiento cero), la energía mecánica total se conserva. La energía se transforma continuamente entre tres tipos:

1. Energía Cinética ($E_c$): La del movimiento. Máxima en el equilibrio. $$ E_c = \frac{1}{2} m v^2 $$

2. Energía Potencial Elástica ($E_{pe}$): La almacenada en el muelle. Máxima en los extremos. $$ E_{pe} = \frac{1}{2} k x^2 $$

3. Energía Potencial Gravitatoria ($E_{pg}$): La debida a la altura. Máxima en el punto más alto. $$ E_{pg} = m g h $$

En la simulación: La "Gráfica de Energías" es la herramienta perfecta para ver esto. Observa cómo las barras suben y bajan, pero la barra de "Total" permanece constante.

¿Qué hace el "Amortiguamiento" y cómo afecta a la energía?

El amortiguamiento representa las fuerzas de fricción. Cuando lo activas, introduces una fuerza que disipa la energía mecánica, convirtiéndola en calor. Por eso la oscilación se detiene.

En la simulación: Pon el amortiguamiento en "Bajo" o "Alto" y observa la "Gráfica de Energías". Verás cómo la barra de Energía Total disminuye gradualmente. La energía no se destruye, solo se transforma en una forma no mecánica.

¿Cómo se determina la rapidez de la oscilación (Período)?

El Período ($T$) es el tiempo que tarda la masa en completar una oscilación completa (ida y vuelta). Se mide en segundos. En un sistema masa-resorte ideal, se calcula con la fórmula:

$$ T = 2\pi \sqrt{\frac{m}{k}} $$

Lo más interesante de esta fórmula es lo que nos dice:

  • A mayor masa ($m$), más lento oscila (mayor período).
  • A mayor rigidez ($k$), más rápido oscila (menor período).
  • ¡El período NO depende de la gravedad ($g$) ni de la amplitud (cuánto lo estires inicialmente)!

En la simulación: Usa el "Cronómetro" para medir el tiempo de 10 oscilaciones y luego divide por 10 para obtener el período. Comprueba que si cambias de la Tierra a la Luna, ¡el período no cambia!

¿Para qué sirve el modo "Dos Muelles"? ¡A experimentar!

El modo "Dos Muelles" es la herramienta más potente de este simulador masa-resorte interactivo. Te convierte en un científico real, permitiéndote realizar experimentos controlados. La idea es cambiar solo una variable a la vez y observar el efecto.

Aquí tienes algunas ideas para tus experimentos:

  1. Experimento 1: Influencia de la Masa
    • Configuración: Muelle 1 y Muelle 2 con la misma constante $k$ (ej: 50 N/m) y en el mismo planeta (Tierra).
    • Variable: Pon una masa pequeña en el Muelle 1 (ej: 0.5 kg) y una grande en el Muelle 2 (ej: 2.0 kg).
    • Observa: La masa mayor estira más el muelle (equilibrio más bajo) y oscila mucho más lento (período mayor).
  2. Experimento 2: Influencia de la Rigidez
    • Configuración: Misma masa en ambos muelles (ej: 1.0 kg) y en el mismo planeta.
    • Variable: Pon una constante $k$ baja en el Muelle 1 (blando, ej: 25 N/m) y una $k$ alta en el Muelle 2 (duro, ej: 100 N/m).
    • Observa: El muelle duro apenas se estira y oscila muy rápidamente, mientras que el blando tiene una oscilación amplia y lenta.

Zona de Actividades de tu Profesor

Introduce la clave de acceso que te ha proporcionado tu profesor para cargar la actividad y comenzar a trabajar.

¿Tu última clase con la simulación fue un éxito?

Si has usado una de nuestras simulaciones para crear una actividad que funcionó de maravilla, te invitamos a compartirla. Crear una actividad es muy fácil y tu experiencia puede ser la inspiración que otro docente necesita.

  • 💡 Transforma tu experiencia en un recurso valioso para miles de profes.
  • 🔥 Ayuda a otros a encender la misma pasión que tú lograste en tu aula.
  • 🌍 Forma parte de una comunidad que cree en compartir para crecer juntos.
📤 Subir mi actividad

*Esto es solo para profes. Si lo eres, pide tu acceso.

Otras Simulaciones en Física

No necesitas dar la clase perfecta

Solo necesitas que tus alumnos entiendan. Usa nuestras simulaciones y cambia el chip sin perder tiempo ni energía.

Zona Profe
Comparte con tus compañeros de clase